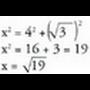Matematika»Geometria
Espazioko geometria
Espazioak hiru dimentsio ditu, eta era askotako plano kopuru
infinitoa hartzen du bere baitan. Baina espazioa aztertzeko abiapuntutzat
hartzen diren axiomak eta erabiltzen diren metodoak planoan
erabilitako berberak dira, eta, beraz, atal honen nondik norakoa
eta aurreko atalena ez da oso bestelakoa izango. Espazioan
gauzaki geometriko berriak eta problema berriak daude ; hiru
dimentsiotan korapilatu egiten dira, oro har, problemak, nahiz
baten bat erraztu ere egiten den. Baina planoaren geometrian ateratzen
diren emaitzak baliozkoak dira espazioko plano guztietan
ere, eta espazioan ateratzen diren emaitza berriek behin ere ez dituzte
ukatzen planoan lortu direnak.Puntuak, zuzenak eta planoak dira espazioko elementu soilenak.
Elementu horiekin egin daitezke poliedroak, aurpegi lauak dituzten
irudiak, alegia, edo egin daitezke irudi, gainalde edo lerro kurbatuak
ere, nola diren konoak, zilindroak eta esferak. Azken hauek
dira kapitulu honetan aztertuko ditugunak. Intzidentzia, paralelismoa,
elkarzutasuna eta antzeko problemak aztertuko dira lehenengo,
eta arestian aipaturiko irudiak, gero.
I. Puntuak, barnekotasun erlazioa.
Planoak eta zuzenak puntu multzoak dira. Baldin eta puntu bat
aztergai den puntu multzoaren barnean badago, esaten da puntu
hori planoaren edo zuzenaren barnean dagoela, edo planoak edo
zuzenak puntu hori daukala. Alderantziz, puntu jakin bat hartuz
gero, puntu horretatik zuzen edo plano multzo oso bat pasatzen da.
Puntu bakarrarekin ezin da irudirik definitu.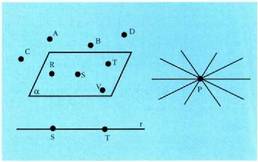
I I. Zuzenak
Zuzen bat definitzeko bi puntu desberdin edo puntu bat eta norabide bat behar dira, planoan bezala. Espazioan, zuzen bat bi planoen ebakidura gisa ere defini daiteke.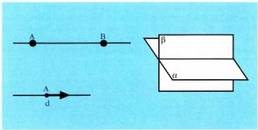 Har dezagun zuzen bat, eta zuzen horretan puntu bat ; puntu
horren ezkerretara edo eskuinetara dauden puntuekin zuzenerdia
egiten da.Har dezagun zuzen bat eta bi puntu ; zuzenki esaten zaio bi puntu
horien artean dagoen zuzeneko puntu multzoari. Hemen ere balio
dute, oro har, planoen atalean eman ziren zuzenki orientatuen,
angeluen, etab.en definizioak.
Har dezagun zuzen bat, eta zuzen horretan puntu bat ; puntu
horren ezkerretara edo eskuinetara dauden puntuekin zuzenerdia
egiten da.Har dezagun zuzen bat eta bi puntu ; zuzenki esaten zaio bi puntu
horien artean dagoen zuzeneko puntu multzoari. Hemen ere balio
dute, oro har, planoen atalean eman ziren zuzenki orientatuen,
angeluen, etab.en definizioak.
Bi zuzenen arteko erlazioa
Har ditzagun bi zuzen -s eta r- ; gerta daiteke :- Bi zuzen horiek bat egitea, baldin eta puntu guztiak komun
badituzte. - Bi zuzen horiek elkar ebakitzea, baldin eta puntu bat badute
komun.
- Bi zuzen horiek elkar ebakitzea, baldin eta puntu bat badute
komun.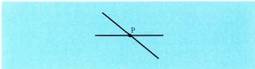 - Bi zuzen horiek paraleloak izatea, baldin eta ez badute punturik
komun eta plano berean badaude.
- Bi zuzen horiek paraleloak izatea, baldin eta ez badute punturik
komun eta plano berean badaude.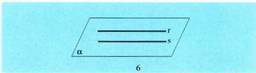 Bi zuzen horiek gurutzatzea, baldin eta ez badute punturik
komun eta ez badaude plano berean.
Bi zuzen horiek gurutzatzea, baldin eta ez badute punturik
komun eta ez badaude plano berean.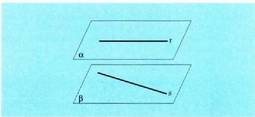 Plano berean dauden zuzenei zuzen planokideak esaten zaie. Bat
egiten duten zuzenak ere zuzen paraleloen multzoan sartu ohi dira,
eta kasu horretan, bat egiten ez duten zuzen paraleloak direla adierazi
nahi denean, esaten da hertsiki paraleloak direla.Kuboaren ertzak dira aukera desberdin horien adibide. ABC-
DEFGH kuboaren ertzek barnean dituzten zuzenei erreparatuz
gero,
Plano berean dauden zuzenei zuzen planokideak esaten zaie. Bat
egiten duten zuzenak ere zuzen paraleloen multzoan sartu ohi dira,
eta kasu horretan, bat egiten ez duten zuzen paraleloak direla adierazi
nahi denean, esaten da hertsiki paraleloak direla.Kuboaren ertzak dira aukera desberdin horien adibide. ABC-
DEFGH kuboaren ertzek barnean dituzten zuzenei erreparatuz
gero,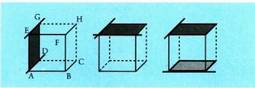 AB eta EF edo DG eta CH paraleloak dira. AB eta BC ertzek eratzen
dituzten zuzenek B puntuan elkar ebakitzen dute. AB eta FB
zuzenak gurutzatu egiten dira.Zuzenen arteko paralelismoak tasun berberak ditu espazioan bezala
planoan ere. Alegia, baldin eta zuzen bat beste baten paraleloa
bada, bigarren zuzena lehenengoaren paraleloa da ; horri lege errefle-
Kiboa esaten zaio. Baldin eta zuzen bat beste baten paraleloa bada, eta
bigarren hori hirugarrenaren paraleloa orobat, lehenengo eta hirugarren
zuzenak ere paraleloak dira. Baldin eta bat egiten duten zuzenak
zuzen paralelotzat jotzen badira, paralelismoak baliokidetasun erla~
!io bat definitzen du zuzen horien artean, zatidura multzotzat espatioan
dauden norabide anitzak dituena. Norabide batean paraleloak
liren zuzen multzoari zuzen paraleloen sorta esaten zaio.Planoan lortzen diren beste emaitza batzuek balio dute espazioan
ere. Hala, bi zuzen ebakitzailek lau angelu definitzen dituzte ;
angelu horiek berdinak dira binaka, erpinean aurkakoak direlako ;
eta angelu pare bakoitzeko angeluak beste parekoen betegarriak
dira, auzokideak direlako. Beste adibide bat, baldin eta zuzen ebakitzaile
batek bi zuzen paralelo ebakitzen baditu, angelu korrespondienteak
berdinak dira, txandakako barnekoak eta txandakako
kanpokoak ; eta betegarriak dira angelu auzokideak eta albo berekoak,
barnekoak edo kanpokoak. Era berean, puntu bat eta zuzen
bat emanik, puntu horretatik zuzen horren zuzen paralelo bakarra
pasa daiteke.Zuzen elkarzutak edo ortogonalak esaten zaie 90°ko angeluen
arabera elkar ebakitzen duten zuzenei. Espazioan bi zuzenek norabide
elkarzutak izan ditzakete, baina ez dute zertan elkarzutak izanik,
elkar ebakitzen ez duten bitartean. Gainera, zuzen bateko
puntu batean elkarzut infinitoak daude, ez bakarra, planoan gertatzen
den bezala.
AB eta EF edo DG eta CH paraleloak dira. AB eta BC ertzek eratzen
dituzten zuzenek B puntuan elkar ebakitzen dute. AB eta FB
zuzenak gurutzatu egiten dira.Zuzenen arteko paralelismoak tasun berberak ditu espazioan bezala
planoan ere. Alegia, baldin eta zuzen bat beste baten paraleloa
bada, bigarren zuzena lehenengoaren paraleloa da ; horri lege errefle-
Kiboa esaten zaio. Baldin eta zuzen bat beste baten paraleloa bada, eta
bigarren hori hirugarrenaren paraleloa orobat, lehenengo eta hirugarren
zuzenak ere paraleloak dira. Baldin eta bat egiten duten zuzenak
zuzen paralelotzat jotzen badira, paralelismoak baliokidetasun erla~
!io bat definitzen du zuzen horien artean, zatidura multzotzat espatioan
dauden norabide anitzak dituena. Norabide batean paraleloak
liren zuzen multzoari zuzen paraleloen sorta esaten zaio.Planoan lortzen diren beste emaitza batzuek balio dute espazioan
ere. Hala, bi zuzen ebakitzailek lau angelu definitzen dituzte ;
angelu horiek berdinak dira binaka, erpinean aurkakoak direlako ;
eta angelu pare bakoitzeko angeluak beste parekoen betegarriak
dira, auzokideak direlako. Beste adibide bat, baldin eta zuzen ebakitzaile
batek bi zuzen paralelo ebakitzen baditu, angelu korrespondienteak
berdinak dira, txandakako barnekoak eta txandakako
kanpokoak ; eta betegarriak dira angelu auzokideak eta albo berekoak,
barnekoak edo kanpokoak. Era berean, puntu bat eta zuzen
bat emanik, puntu horretatik zuzen horren zuzen paralelo bakarra
pasa daiteke.Zuzen elkarzutak edo ortogonalak esaten zaie 90°ko angeluen
arabera elkar ebakitzen duten zuzenei. Espazioan bi zuzenek norabide
elkarzutak izan ditzakete, baina ez dute zertan elkarzutak izanik,
elkar ebakitzen ez duten bitartean. Gainera, zuzen bateko
puntu batean elkarzut infinitoak daude, ez bakarra, planoan gertatzen
den bezala.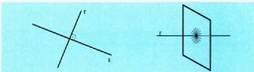 Puntu batek zuzen baten gainean egiten duen proiekzioa : zuzen
horrek eta puntu horretatik pasatzen den haren perpendikularrak
elkar ebakitzen duten puntua. Espazioan zuzen perpendikularra
nekez aurkitzen denez, puntutik pasatzen den zuzenaren plano perpendikularra
erabiltzen da, zuzen perpendikularra plano horren
barnean baitago.
Puntu batek zuzen baten gainean egiten duen proiekzioa : zuzen
horrek eta puntu horretatik pasatzen den haren perpendikularrak
elkar ebakitzen duten puntua. Espazioan zuzen perpendikularra
nekez aurkitzen denez, puntutik pasatzen den zuzenaren plano perpendikularra
erabiltzen da, zuzen perpendikularra plano horren
barnean baitago.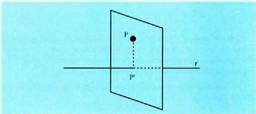 Puntu batetik zuzen batera dagoen distantzia : puntu horretatik
zuzen horretako puntu bakoitzera dagoen distantzien artean txikiena
da. Distantzia txikiena, planoan bezala, bat dator puntuaren eta
puntuak zuzenaren gainean egiten duen proiekzioaren artean dagoen
distantziarekin, zeren eta zuzenki elkarzut bat zuzenki zeihar bat
baino txikiagoa baita beti.
Puntu batetik zuzen batera dagoen distantzia : puntu horretatik
zuzen horretako puntu bakoitzera dagoen distantzien artean txikiena
da. Distantzia txikiena, planoan bezala, bat dator puntuaren eta
puntuak zuzenaren gainean egiten duen proiekzioaren artean dagoen
distantziarekin, zeren eta zuzenki elkarzut bat zuzenki zeihar bat
baino txikiagoa baita beti.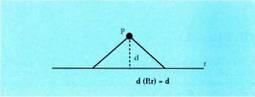 Bi zuzenen arteko distantzia esaten zaio lehenengo zuzeneko
puntu baten eta bigarren zuzeneko puntu baten artean dagoen
distantzia txikienari. Zuzen ebakitzaileen edo bat egiten duten
zuzenen arteko distantzia zero da. Baldin eta zuzenak paraleloak
badira, paralelo horiek perpendikular batean ebakitzen duten
zuzenkia da distantzia txikiena, eta, beraz, hori da paraleloen arteko
distantzia.
Bi zuzenen arteko distantzia esaten zaio lehenengo zuzeneko
puntu baten eta bigarren zuzeneko puntu baten artean dagoen
distantzia txikienari. Zuzen ebakitzaileen edo bat egiten duten
zuzenen arteko distantzia zero da. Baldin eta zuzenak paraleloak
badira, paralelo horiek perpendikular batean ebakitzen duten
zuzenkia da distantzia txikiena, eta, beraz, hori da paraleloen arteko
distantzia.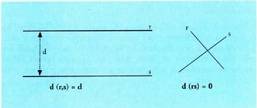 Baldin eta zuzenak gurutzatzen badira, distantzia ere elkarzut
komunean eratzen duten zuzenkiari dagokio.
Baldin eta zuzenak gurutzatzen badira, distantzia ere elkarzut
komunean eratzen duten zuzenkiari dagokio.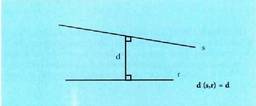
- Ariketak
1. Bilatu kuboan paraleloak diren, gurutzatzen diren edo elkar ebakitzen duten zuzenen beste bi adibide.
I I I. Planoak
Plano bat muga daiteke lerrokatuta ez dauden hiru punturen
bidez, edo zuzen batez eta zuzen horretan ez dagoen puntu batez,
edo bi zuzen ebakitzailez, edo bi zuzen hertsiki paraleloz, edo puntu
batez eta bi norabide desberdinez.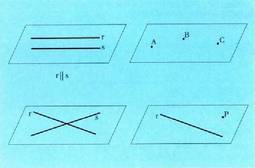 Hala ere, 4 puntuk ez dute beti plano bat mugatzen, 4 punturekin
tetraedro bat egin daiteke eta. Era berean, gurutzatzen diren bi
zuzen abiapuntutzat harturik ezin daiteke planorik eratu, baina
tetraedro bat egin liteke.
Hala ere, 4 puntuk ez dute beti plano bat mugatzen, 4 punturekin
tetraedro bat egin daiteke eta. Era berean, gurutzatzen diren bi
zuzen abiapuntutzat harturik ezin daiteke planorik eratu, baina
tetraedro bat egin liteke.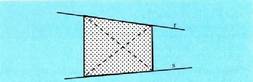 Zuzen batek bakarrik ez du plano bat finkatzen, plano sorta infinitu
batek izan dezakeelako barnean zuzen hori.
Zuzen batek bakarrik ez du plano bat finkatzen, plano sorta infinitu
batek izan dezakeelako barnean zuzen hori. Plano bat adierazteko a b g p etab. letra grekoak erabiltzen dira,
edo, bestela, planoan dauden hiru puntuko letrak, adibidez, ABC.
Plano bat adierazteko a b g p etab. letra grekoak erabiltzen dira,
edo, bestela, planoan dauden hiru puntuko letrak, adibidez, ABC.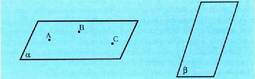 Plano batek bi azpiespazio desberdinetan banatzen du espazioa ;
puntu bat planoaren alde batean edo bestean egon, hartara egongo
da azpiespazio batean edo bestean ere.
Plano batek bi azpiespazio desberdinetan banatzen du espazioa ;
puntu bat planoaren alde batean edo bestean egon, hartara egongo
da azpiespazio batean edo bestean ere.
Zuzenki baten plano erdibitzailea.
Zuzenki bat hartuz gero, zuzen erdibitzailea erdiko puntuko
zuzen elkarzutetako baten bidez defini daiteke, baina hobe da
plano erdibitzailea definitzea. Izan ere, zuzen erdibitzailea ez da
bakarra, zuzen erdibitzaile sorta oso bat dago. Zuzenki baten
muturretatik distantzia berera dauden espazioko puntuen leku
geometrikoa da, erdiko puntuan, zuzenki horri buruz zut dagoen
planoa. Plano horrek zuzen erdibitzaile guztiak dauzka barnean
.Hori frogatzeko, plano horretako edozein puntuk muturretatik distantzia bera duela ikusiko da aurrena. Horretarako, demagun edozein puntu -P- ; puntu hori plano erdibitzaileak zuzenkia ebakitzen duen puntuarekin lotzen duen zuzen bat -PM- marrazten da.
Puntu horretatik zuzenkiaren erpin batera ber bi dagoen distantzia, ebakitze punturainoko zuzenkiaren zatiaren berbiduren batura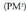 gehi ebakitze puntutik muturreraino gelditzen den zuzenki zatiaren berbiduraren
gehi ebakitze puntutik muturreraino gelditzen den zuzenki zatiaren berbiduraren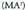 berdina da, planoa perpendikularra da eta eratzez, eta bilatzen ari garen distantziak bi triangelu zuzenen hipotenusak dira eta. Baina bi triangelu zuzen horiek badute katetu bat, planoan dagoena (PM), berdina dena komuna delako ; eta bestea (MA eta MB), zatitutako zuzenkian dagoena, berdina da baita ere, zuzenkia erdibitua dagoelako. Beraz, hipotenusak berdinak dira, eta distantzia bera dago adierazitako puntu horretatik muturretara.Alderantziz, baldin eta puntu horretatik muturretara distantzia
bera badago, puntu hori planoan dago. Demagun puntu bat, P,
muturretara distantzia bera duena ; zuzen elkarzuta egiten da
zuzenkiraino, PM ; zuzen horrek erdiko puntuan ebaki behar du
zuzenkia, bestela distantziak ez bailirateke berdinak izango, distantzia
horiek direlarik PM aldea komun duten APM eta BPM
triangelu zuzenen AP eta BP hipotenusak. Baina plano bakarra
dago AB zuzenkiarekiko elkarzuta dena, erdiko puntutik ; beraz, P
plano erdibitzailean dago, eta hori da hain zuzen frogatu nahi
genuena.
berdina da, planoa perpendikularra da eta eratzez, eta bilatzen ari garen distantziak bi triangelu zuzenen hipotenusak dira eta. Baina bi triangelu zuzen horiek badute katetu bat, planoan dagoena (PM), berdina dena komuna delako ; eta bestea (MA eta MB), zatitutako zuzenkian dagoena, berdina da baita ere, zuzenkia erdibitua dagoelako. Beraz, hipotenusak berdinak dira, eta distantzia bera dago adierazitako puntu horretatik muturretara.Alderantziz, baldin eta puntu horretatik muturretara distantzia
bera badago, puntu hori planoan dago. Demagun puntu bat, P,
muturretara distantzia bera duena ; zuzen elkarzuta egiten da
zuzenkiraino, PM ; zuzen horrek erdiko puntuan ebaki behar du
zuzenkia, bestela distantziak ez bailirateke berdinak izango, distantzia
horiek direlarik PM aldea komun duten APM eta BPM
triangelu zuzenen AP eta BP hipotenusak. Baina plano bakarra
dago AB zuzenkiarekiko elkarzuta dena, erdiko puntutik ; beraz, P
plano erdibitzailean dago, eta hori da hain zuzen frogatu nahi
genuena.
Bi planoen posizio erlatiboak.
Demagun badirela bi plano, ; plano horiek izan daitezke :Bat datozenak, baldin eta puntu guztiak komun badituzte.
; plano horiek izan daitezke :Bat datozenak, baldin eta puntu guztiak komun badituzte. Paraleloak, baldin eta puntu bat bera ere ez badute komun..
Paraleloak, baldin eta puntu bat bera ere ez badute komun.. 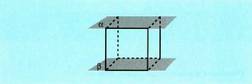 Ebakitzaileak, baldin eta zuzen baten arabera elkar ebakitzen
badute.
Ebakitzaileak, baldin eta zuzen baten arabera elkar ebakitzen
badute.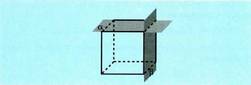 Horregatik, bi plano ebakitzailek zuzen bat definitzen dute.
Horregatik, bi plano ebakitzailek zuzen bat definitzen dute.
Baina zuzen bat hartuz gero, zuzen hori ez dute bi plano jakinek
bakarrik definitzen, zuzen horretatik pasatzen den plano sortako
edozein plano parek baizik.Paralelismo erlazioa erreflexiboa, simetrikoa eta iragankorra da ;
eta puntu eta plano bat emanik espazioan, plano horren plano paralelo
bakarra pasa daiteke puntu horretatik.Elkar ebakitzen duten bi planok lau zatitan zatitzen dute espazioa.
Horietako espazio bakoitzari angelu diedroa esaten zaio ; alegia,
espazioan agertzen den angelu mota berri bat da.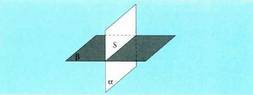 Baldin eta hiru plano edo gehiago badaude, aukera asko dira.
Baldin eta hiru plano edo gehiago badaude, aukera asko dira.
Puntu batean elkar ebaki dezakete, eta angelu poliedro bat eratu ;
edo zuzen batean ebaki dezakete elkar, eta plano sorta berekoak
izan ; edo hiru planoak paraleloak izan daitezke ; edo bi paraleloak
eta hirugarrena ebakitzailea ere izan daitezke, etab.
Planoaren eta zuzenaren arteko erlazioa
Planoek badute ezaugarri bat : plano bateko bi puntu zuzen baten
barnean badaude, zuzen oso hori planoaren baitan dago. Planoak
berezkoa du ezaugarri hori, eta ezaugarri horretxek bereizten du planoa
beste gainaldeetatik.Hauek dira zuzenaren eta planoaren kokaera erlatiboak :Zuzena planoaren barnean egotea, zuzen hori denean zuzenaren
eta planoaren ebaketa.Zuzenak eta planoak puntu batean elkar ebakitzea.Zuzenak eta planoak batere punturik komun ez izan eta elkarren
paralelo izatea.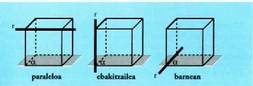 Baldin eta zuzen bat plano baten paraleloa bada, zuzen horren
paraleloak diren zuzen kopuru infinitoa dago plano horren barnean.
Baldin eta zuzen bat plano baten paraleloa bada, zuzen horren
paraleloak diren zuzen kopuru infinitoa dago plano horren barnean.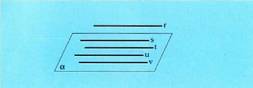 Baldin eta plano batek zuzen bat ebakitzen badu, orobat ebakitzen
du zuzen horren paraleloa den zuzen oro. Baldin eta zuzen
batek plano bat ebakitzen badu, orobat ebakitzen ditu plano horren
paraleloak diren planoak.
Baldin eta plano batek zuzen bat ebakitzen badu, orobat ebakitzen
du zuzen horren paraleloa den zuzen oro. Baldin eta zuzen
batek plano bat ebakitzen badu, orobat ebakitzen ditu plano horren
paraleloak diren planoak.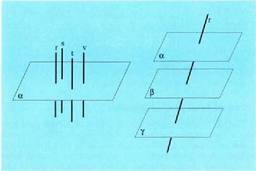 Zuzen baten paraleloak diren planoek elkar ebaki dezakete. Plano
baten paraleloak diren eta puntu batetik pasatzen diren zuzen guztiek
puntu horretatik pasatzen den plano paralelo bat eratzen dute.
Zuzen baten paraleloak diren planoek elkar ebaki dezakete. Plano
baten paraleloak diren eta puntu batetik pasatzen diren zuzen guztiek
puntu horretatik pasatzen den plano paralelo bat eratzen dute.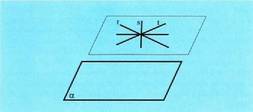 Baldin eta zuzen batek plano bat ebakitzen badu, orobat ebakitzen
ditu ebakitze puntutik pasatzen diren planoko zuzen guztiak.
Baldin eta zuzen batek plano bat ebakitzen badu, orobat ebakitzen
ditu ebakitze puntutik pasatzen diren planoko zuzen guztiak.
Zuzen horiek eta emandako zuzenak angeluak eratuko dituzte, eta
ebakitze puntutik pasatzen den zuzena nolakoa den, halakoa izango
da angelu horren balioa. Zuzenaren eta planoaren arteko angelua
esaten zaio angelu horien artean txikienari. Ebakitze puntutik
pasatzen diren gainerako zuzenekin eratutako angeluak gero eta
handiagoak izango dira, harik eta zuzen batekin eratutako angelua
90°koa izango den arte ; gero, angeluak aurreko angeluen betegarriak
izango dira.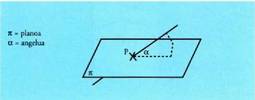 Zuzen bat plano bati buruz zuta da, zuzen horrek eta ebakitze
puntutik pasatzen diren zuzen guztiek eratzen duten angelua
90°koa baldin bada. Zuzen horri eta plano horri ortogonal edo
elkarzut esaten zaie, eta honela adierazten da : r Ia.
Zuzen bat plano bati buruz zuta da, zuzen horrek eta ebakitze
puntutik pasatzen diren zuzen guztiek eratzen duten angelua
90°koa baldin bada. Zuzen horri eta plano horri ortogonal edo
elkarzut esaten zaie, eta honela adierazten da : r Ia.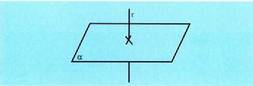 Baldin eta zuzen bat plano bati buruz zuta bada, zuzen hori zuta
da orobat plano horren plano paralelo guztiei buruz.Baldin eta plano bat zuzen bati buruz zuta bada, plano hori zuta
da orobat zuzen horren paralelo guztiei buruz.
Baldin eta zuzen bat plano bati buruz zuta bada, zuzen hori zuta
da orobat plano horren plano paralelo guztiei buruz.Baldin eta plano bat zuzen bati buruz zuta bada, plano hori zuta
da orobat zuzen horren paralelo guztiei buruz.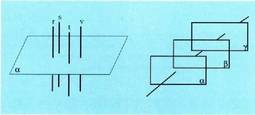 Alderantziz, plano berari buruz zutak diren zuzenak paraleloak
dira elkarri buruz ere.Puntu bat eta plano bat harturik, puntu horretatik plano hori
ebakitzen duen zuzen zut bat eginez gero, zuzen horrek planoa ebakitzen
duen puntua da puntuaren proiekzio ortogonala.Harturik zuzen bat eta plano bat ; zuzen horretako puntu guztien
proiekzio guztiak barnean dituen zuzena da hasierako zuzenaren
proiekzio ortogonala.
Alderantziz, plano berari buruz zutak diren zuzenak paraleloak
dira elkarri buruz ere.Puntu bat eta plano bat harturik, puntu horretatik plano hori
ebakitzen duen zuzen zut bat eginez gero, zuzen horrek planoa ebakitzen
duen puntua da puntuaren proiekzio ortogonala.Harturik zuzen bat eta plano bat ; zuzen horretako puntu guztien
proiekzio guztiak barnean dituen zuzena da hasierako zuzenaren
proiekzio ortogonala.
Puntu baten eta plano baten arteko distantzia.
Puntu baten eta plano baten arteko distantzia : puntu jakin
baten eta planoko puntuen arteko distantzia txikiena da. Puntubaten eta plano baten arteko distantzia bat dator puntu baten eta
puntu horrek planoan duen proiekzioaren arteko distantziarekin
.Puntua planoan baldin badago, distantzia hori zero da.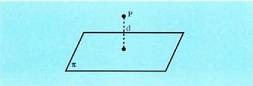 Kanpoko puntu baten eta planoko puntuen arteko distantzia
konstantea denean, planoko puntu horiek zirkunferentzia zentrukidetan
daude proiekzioaren inguruan.
Kanpoko puntu baten eta planoko puntuen arteko distantzia
konstantea denean, planoko puntu horiek zirkunferentzia zentrukidetan
daude proiekzioaren inguruan.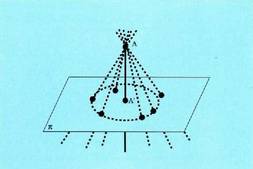 Zuzen baten eta plano baten arteko distantzia : zuzen horretako
puntuen eta plano horretako puntuen artean dagoen distantziarik
txikiena da. Distantzia hori zero da, baldin eta zuzen hori eta plano
hori paraleloak ez badira ; paraleloak badira berriz, distantzia hori
bat dator zuzen horretako edozein punturen eta planoaren arteko
distantziarekin.
Zuzen baten eta plano baten arteko distantzia : zuzen horretako
puntuen eta plano horretako puntuen artean dagoen distantziarik
txikiena da. Distantzia hori zero da, baldin eta zuzen hori eta plano
hori paraleloak ez badira ; paraleloak badira berriz, distantzia hori
bat dator zuzen horretako edozein punturen eta planoaren arteko
distantziarekin.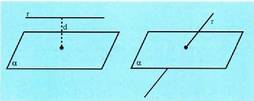 Bi planoren arteko distantzia: plano bateko eta besteko puntuen
arteko distantzia txikiena da. Distantzia hori zero da, baldin eta bi
plano horiek paraleloak ez badira ; paraleloak badira berriz, distantzia
hori plano bateko edozein punturen eta beste planoaren arteandagoen distantzia bera da ; alegia, distantzia hori bi planoen artean
dagoen perpendikular komunaren luzeraren berdina da.
Bi planoren arteko distantzia: plano bateko eta besteko puntuen
arteko distantzia txikiena da. Distantzia hori zero da, baldin eta bi
plano horiek paraleloak ez badira ; paraleloak badira berriz, distantzia
hori plano bateko edozein punturen eta beste planoaren arteandagoen distantzia bera da ; alegia, distantzia hori bi planoen artean
dagoen perpendikular komunaren luzeraren berdina da.
- Ariketak
2. Bilatu kubo batean bi plano erdibitzaile eta bi plano
paralelo.3. Bilatu kubo bateko AB ertza erdibitzen duen planoa ;
bilatu ertz hori erdibituko duten bi zuzen ere.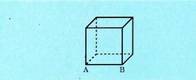 4. Baldin eta M kubo bateko BCFG planoko puntu bat
bada, frogatu M puntua eta G eta B lerrokatuta daudela,
baldin eta AH eta M erpinek definitutako planoa
ADEH planoari buruz zuta bada.
4. Baldin eta M kubo bateko BCFG planoko puntu bat
bada, frogatu M puntua eta G eta B lerrokatuta daudela,
baldin eta AH eta M erpinek definitutako planoa
ADEH planoari buruz zuta bada.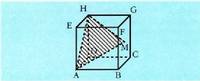 5. ABCD tetraedro batean, P puntu bat hartzen da AB
ertzean, eta Q puntu bat, AC ertzean ; baldin eta PQ eta
BC zuzenek M puntuan elkar ebakitzen badute, non
ebakiko dute elkar BCD eta PQD planoek?
5. ABCD tetraedro batean, P puntu bat hartzen da AB
ertzean, eta Q puntu bat, AC ertzean ; baldin eta PQ eta
BC zuzenek M puntuan elkar ebakitzen badute, non
ebakiko dute elkar BCD eta PQD planoek?
I V. Angelu diedroak eta poliedroak
Elkar ebakitzen duten bi planok lau eremu mugatzen dituzte
espazioan ; eremu bakoitzari angelu diedroa esaten zaio.Bi planoerdiek komun duten zuzenari ertza esaten zaio, eta planoerdi
bakoitza angelu diedroaren alde bat da.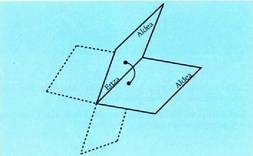 Angelu diedroa neurtzeko, bi planoerdiak ertzarekiko elkarzuta
den plano batez ebakitzen dira. Epai hori ertzarekiko zutak diren bi
zuzenek eratzen dute ; eta bi zuzen horiek ertzarekin eratzen duten
angeluari diedroaren lerrozuzena esaten zaio.
Angelu diedroa neurtzeko, bi planoerdiak ertzarekiko elkarzuta
den plano batez ebakitzen dira. Epai hori ertzarekiko zutak diren bi
zuzenek eratzen dute ; eta bi zuzen horiek ertzarekin eratzen duten
angeluari diedroaren lerrozuzena esaten zaio.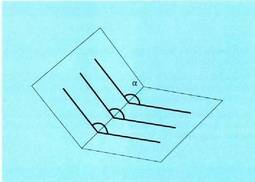 Bi zuzenerdiak, bakoitza planoerdi batean, ertzarekiko elkarzutak
dira puntu berean. Baldin eta ez badira bi zuzen elkarzut horiek
hartzen, bi zuzenerdik, edozeinek, bata plano batekoa eta bestea
bestekoa, eratzen duten angeluak edozein kopuru balio dezake,
angelu baliogabetik (0°) angelu lauraino (180°).Angelu lauetan gertatzen den bezala, angelu diedroaren lerrozuzena
180° baino handiagoa edo txikiagoa izan, hala izango da ahurra
ala ganbila ere.Diedro betegarria eta osagarria dagokie lerrozuzenak betegarriak
edo osagarriak dituzten angeluei. Diedro auzokideak betegarriak
dira. Diedro zuzenak plano elkarzutei dagozkie. Diedro kamutsak
edo zorrotzak ere defini daitezke.
Bi zuzenerdiak, bakoitza planoerdi batean, ertzarekiko elkarzutak
dira puntu berean. Baldin eta ez badira bi zuzen elkarzut horiek
hartzen, bi zuzenerdik, edozeinek, bata plano batekoa eta bestea
bestekoa, eratzen duten angeluak edozein kopuru balio dezake,
angelu baliogabetik (0°) angelu lauraino (180°).Angelu lauetan gertatzen den bezala, angelu diedroaren lerrozuzena
180° baino handiagoa edo txikiagoa izan, hala izango da ahurra
ala ganbila ere.Diedro betegarria eta osagarria dagokie lerrozuzenak betegarriak
edo osagarriak dituzten angeluei. Diedro auzokideak betegarriak
dira. Diedro zuzenak plano elkarzutei dagozkie. Diedro kamutsak
edo zorrotzak ere defini daitezke.
Angelu poliedroak
Angelu poliedroa: erpin izeneko puntu batean elkartzen diren
hiru planok edo gehiagok mugaturiko espazioko eremua da. Alde
bakoitza angelu poliedroaren aurpegi bat da.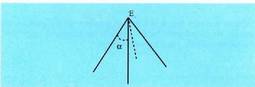 Angelu poliedroetan, aurpegiak angelu lauaren arabera neurtzen
dira, eta ondoz ondoko bi aurpegien artean angelu diedro bat dago.
Angelu poliedroetan, aurpegiak angelu lauaren arabera neurtzen
dira, eta ondoz ondoko bi aurpegien artean angelu diedro bat dago.
Hiru alde baino gehiago dituzten angelu poliedroak ahurrak edo
ganbilak izan daitezke.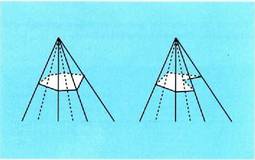 Angelu poliedro erabiliena triedro zuzena da, aurpegiek elkarrekin
diedro zuzenak eratzen dituztenak eta diedro epaiek ere elkarrekin
angelu zuzenak eratzen dituztenak, alegia.
Angelu poliedro erabiliena triedro zuzena da, aurpegiek elkarrekin
diedro zuzenak eratzen dituztenak eta diedro epaiek ere elkarrekin
angelu zuzenak eratzen dituztenak, alegia.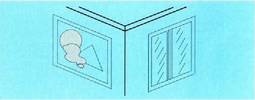
V. Pitagorasen teorema espazioan.
Pitagorasen teoremak espazioan ere balio du, planoko beste teoremek
balio duten bezalaxe. Triangelu bat, ABC, harturik :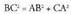 Espazioko geometrian hiru norabide elkarzutekin lan egiten da
maiz, eta, beraz, erosoagoa izaten da sarritan hiru norabide elkarzutetan
dauden eta B eta C elkartzen dituzten hiru zuzenki erabiltzea,
triangelu zuzeneko bi katetoak erabiltzea baino.
Espazioko geometrian hiru norabide elkarzutekin lan egiten da
maiz, eta, beraz, erosoagoa izaten da sarritan hiru norabide elkarzutetan
dauden eta B eta C elkartzen dituzten hiru zuzenki erabiltzea,
triangelu zuzeneko bi katetoak erabiltzea baino.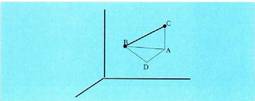 Demagun BA dela BDA triangelu zuzenaren hipotenusa, horren
arabera :
Demagun BA dela BDA triangelu zuzenaren hipotenusa, horren
arabera :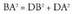 Eta, beraz, Pitagorasen teorema honela geldituko litzateke :
Eta, beraz, Pitagorasen teorema honela geldituko litzateke :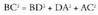
- Ariketak
6. Aldean 2 banako dituen kubo baten erpinen arteko distantzia aurkitu.7. Ertzean "L" banako dituen kubo batean, aurkitu ertz baten erdiko puntutik 8 erpinetara dagoen distantzia.
V I. Poliedroak
Poliedroa gorputz geometriko bat da, poligono diren lau aldek
edo gehiagok mugatua. Poliedroak gainalde lauez itxitako gorputz
gotor itxiak dira ; esferak, konoak eta gainalde kurboz mugatuta
dauden beste irudi batzuk ez dira poliedroak.Aurpegiak beren aldeen arabera lotzen zaizkio elkarri, eta poliedroaren
ertzak eratzen dituzte. Aldameneko bi aurpegik angelu diedro
bat eratzen dute. Poligonoen erpinak bat datoz puntu batzuetan
; puntu horiek poliedroaren erpinak dira. Poliedroaren erpin
horietan angelu poliedroak eratzen dira. Poliedroak ganbilak ala ahurrak izan daitezke. Poliedro ganbilek
teorema hau betetzen dute :Euler-en teorema :Poliedro ganbil guztietan egiaztatzen da aurpegi (C) kopurua gehi
erpin (V) kopurua ertz (A) kopurua gehi bi dela.
Poliedroak ganbilak ala ahurrak izan daitezke. Poliedro ganbilek
teorema hau betetzen dute :Euler-en teorema :Poliedro ganbil guztietan egiaztatzen da aurpegi (C) kopurua gehi
erpin (V) kopurua ertz (A) kopurua gehi bi dela.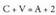 Teorema hori frogatzeko Schlegel-en diagramak erabiltzen dira ;
eta, hala, ikusten da aurpegi baten erdigune gainetik ikusiko litzatekeena,
baldin eta ertzak bakarrik ikusiko balira.
Teorema hori frogatzeko Schlegel-en diagramak erabiltzen dira ;
eta, hala, ikusten da aurpegi baten erdigune gainetik ikusiko litzatekeena,
baldin eta ertzak bakarrik ikusiko balira.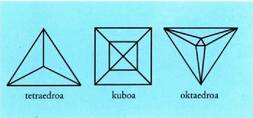 Horrelako diagrama batean, aurpegi batek bi eremutan -r- zatituko
luke planoa, eta nola poligono bat den, ertz -a- bezainbat
erpin -v- izango lituzke. Beraz, hau beteko da: r + v = a + 2. Baldin
eta beste aurpegi bat marrazten bada, aurpegi horrek ertz bat eta bi
erpin izan behar ditu aurrekoarekin komun, eta beste eremu bat
erantsi behar zaio planoa zatituta dagoen eremu kopuruari. Ertz
kopurua aztertzen ari garen poligonoaren ertz kopurua ken batez
handituko da, zeren eta ertz bat baitu komun aurreko aurpegiarekin
. Erpin kopurua aurpegi berriaren erpin kopurua ken bi izango
da, zeren eta bi erpin aurreko poligonoan baitzeuden. Beraz, r + v
= a + 2 balioduna izango litzateke hala ere. Horrela jarrai daiteke
harik eta aurpegien irudikatzeek planoa estaliko duten arte, eta
orduan geratuko den eremu kopurua aurpegi kopuruaren berdina
izango da. Hori zehatzago frogatzeko, edozein poliedro ganbil era
horretako diagrama baten bidez irudika daitekeela frogatu behar
da lehenik, eta erabilitako prozedurak ea edozein poliedro ganbilerako
balio duen ikusi behar da gero.Prismak, piramideak eta poliedro erregularrak dira poliedro ezagunenak
.Prisma poliedro bat da ; bi aurpegi paralelo ditu, oinarri esaten
zaienak, eta bi poligono berdin direnak ; eta gainerako aurpegiak,
alde esaten zaienak, paralelogramoak dira.
Horrelako diagrama batean, aurpegi batek bi eremutan -r- zatituko
luke planoa, eta nola poligono bat den, ertz -a- bezainbat
erpin -v- izango lituzke. Beraz, hau beteko da: r + v = a + 2. Baldin
eta beste aurpegi bat marrazten bada, aurpegi horrek ertz bat eta bi
erpin izan behar ditu aurrekoarekin komun, eta beste eremu bat
erantsi behar zaio planoa zatituta dagoen eremu kopuruari. Ertz
kopurua aztertzen ari garen poligonoaren ertz kopurua ken batez
handituko da, zeren eta ertz bat baitu komun aurreko aurpegiarekin
. Erpin kopurua aurpegi berriaren erpin kopurua ken bi izango
da, zeren eta bi erpin aurreko poligonoan baitzeuden. Beraz, r + v
= a + 2 balioduna izango litzateke hala ere. Horrela jarrai daiteke
harik eta aurpegien irudikatzeek planoa estaliko duten arte, eta
orduan geratuko den eremu kopurua aurpegi kopuruaren berdina
izango da. Hori zehatzago frogatzeko, edozein poliedro ganbil era
horretako diagrama baten bidez irudika daitekeela frogatu behar
da lehenik, eta erabilitako prozedurak ea edozein poliedro ganbilerako
balio duen ikusi behar da gero.Prismak, piramideak eta poliedro erregularrak dira poliedro ezagunenak
.Prisma poliedro bat da ; bi aurpegi paralelo ditu, oinarri esaten
zaienak, eta bi poligono berdin direnak ; eta gainerako aurpegiak,
alde esaten zaienak, paralelogramoak dira.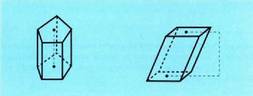 Prismak beren oinarrien poligonoen arabera sailkatzen dira :
triangeluarrak, tetragonalak, pentagonalak, etab.
Prismak beren oinarrien poligonoen arabera sailkatzen dira :
triangeluarrak, tetragonalak, pentagonalak, etab.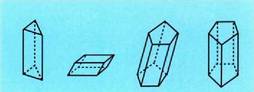 Prismaren oinarrietako planoen arteko distantziari prismaren
alturari esaten zaio.Prismak zuzenak ala zeiharrak izan daitezke. Alboko aurpegiak
oinarriari buruz zutak badira, zuzenak dira; zutak ez badira, zeiharrak
.Prisma erregularrak : oinarriak poligono erregular dituzten prisma
zuzenak dira.
Prismaren oinarrietako planoen arteko distantziari prismaren
alturari esaten zaio.Prismak zuzenak ala zeiharrak izan daitezke. Alboko aurpegiak
oinarriari buruz zutak badira, zuzenak dira; zutak ez badira, zeiharrak
.Prisma erregularrak : oinarriak poligono erregular dituzten prisma
zuzenak dira.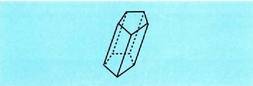 Paralelepipedoak oinarriak paralelogramo dituzten prismak dira.
Paralelepipedoak oinarriak paralelogramo dituzten prismak dira.
Aurpegi guztiak laukizuzenak baldin baditu, ortoedro esaten zaio ;
aurpegi guztiak laukiak baldin baditu, berriz, kubo.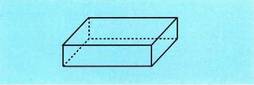 Orobat esan daiteke prismak gainalde prismatiko batez, zuzen bat
poligono bati jarraiki paraleloki mugitzean sortzen den gainaldeaz,
alegia, eta gainalde prismatiko hori ebakitzen duten bi plano paraleloz
eratuta daudela.Piramideak oinarria poligono batez, edozeinez, osatua, eta gainerako
aurpegiak piramidearen erpin esaten zaion puntu batean
elkartzen diren triangeluz osatuak dituen poliedroak dira.
Orobat esan daiteke prismak gainalde prismatiko batez, zuzen bat
poligono bati jarraiki paraleloki mugitzean sortzen den gainaldeaz,
alegia, eta gainalde prismatiko hori ebakitzen duten bi plano paraleloz
eratuta daudela.Piramideak oinarria poligono batez, edozeinez, osatua, eta gainerako
aurpegiak piramidearen erpin esaten zaion puntu batean
elkartzen diren triangeluz osatuak dituen poliedroak dira.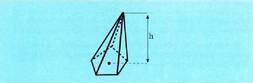 Piramideak oinarriko poligonoaren alde kopuruaren arabera sailkatzen
dira.
Piramideak oinarriko poligonoaren alde kopuruaren arabera sailkatzen
dira.
Piramidearen altuera erpinaren eta oinarriaren arteko distantziari
esaten zaio.
Piramide zuzena aurpegiak triangelu isoszeleak dituenari esaten
zaio ; aurpegiren bat eskalenoa baldin badu, piramide hori zeiharra da.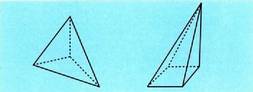 Oinarria poligono erregular bat duen piramide zuzenari piramide
erregularra esaten zaio. Piramide erregular baten alboko aurpegien
altuerari apotema esaten zaio.
Oinarria poligono erregular bat duen piramide zuzenari piramide
erregularra esaten zaio. Piramide erregular baten alboko aurpegien
altuerari apotema esaten zaio.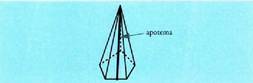 Piramidearen enborra oinarriaren eta oinarriari buruz paraleloa
den plano baten arteko piramidearen zatiak eratzen duen irudiari
esaten zaio.
Piramidearen enborra oinarriaren eta oinarriari buruz paraleloa
den plano baten arteko piramidearen zatiak eratzen duen irudiari
esaten zaio.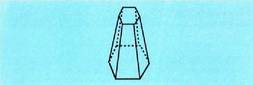 Poliedro bat garatzea haren aurpegiak plano baten gainean
marraztea da. Poliedroa plano baten gainean zabaltzeko moduan
ertzetatik ebakitzea bezala da. Poliedroak era askotara gara daitezke.
Poliedro bat garatzea haren aurpegiak plano baten gainean
marraztea da. Poliedroa plano baten gainean zabaltzeko moduan
ertzetatik ebakitzea bezala da. Poliedroak era askotara gara daitezke.
Garapen horiek oso baliagarriak izaten dira aurpegien tankera jakiteko
eta poliedroen azalera kalkulatzeko, eta azalera arautua duten
gorputz geometrikoetarako, konoetarako edo zilindroetarako, adibidez.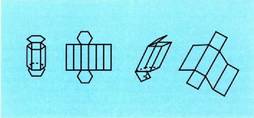
- Ariketak
8. Zenbat ertz eta erpin ditu oinarria laukia duen piramide batek? Euler-en teorema betetzen du? Gauza bera egizu oinarria hexagono duen piramide enbor batekin.9. Oinarriko ertzean 3 banako dituen eta altueran 4 banako dituen piramide triangeluar erregular baten garapena marraztu.
Cavalieriren perspektiba
Espazioaren geometrian, marrazki industrialean, pintura artistikoan,
kartografian edo argazkigintzan, behar-beharrezko gauza izaten da hiru
dimentsiotako gauzaki bat paperean marraztea.Kasu horietan guztietan proiekzio problema bat izaten da. Ikusmenean
edo argazkigintzan, izpiak hiru dimentsiotako gauzakietatik datozen zuzenak
dira, eta izpi horiek halako moduan ebakitzen dute papera, non gauzakiaren
puntu bakoitzari puntu bana baitagokio planoan. Gauzaki urrunenak
txikiagoak ikusten dira, eta bi paraleloen artean dagoen norbaitek
paralelo horiek urrunean azkenik elkartuko direlako irudipena izaten du.
Efektu horiek erdiko edo puntu batetiko proiekzio baten bidez lortzen
dira. Irudiak nahiko ondo adierazten du gauzakia, baina ez dezake ez
dimentsiorik ez paralelismorik ziurta.Marrazki industrialean, aitzitik, garrantzi handia du pieza bakoitza guztiz
zehatz irudikatzeak, eta, horrexegatik, proiekzio ortogonalak egiteko
joera dago, zeren eta, sakontasuna ondo antzematen ez bada ere proiekzio
horien bidez, irudikatu nahi den planoa zehatz irudikatzen baita planoan,
distantziak aise kalkula daitezkeela, soil-soilik papereko neurrietara dagokien
eskala aplikaturik, eta angeluak zirkuluerdi graduatu batez zuzenean
eramanik. Baina piezak zer itxura duen ondo jakiteko, proiekzio bat baino
gehiago egin behar izaten da.Bi mutur horiek perspektiba konikoari eta proiekzio diedriko bati
legozkioke. Bada tarteko proiekzio bat Cavalieriren perspektiba deritzana,
eta hori da geometriako irudikatzeek hurbilen dutena.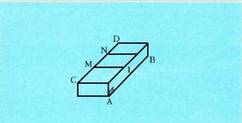 Cavalieriren perspektiban proiekzioa norabide baten arabera egiten da,
baina norabide hori ez dago marrazkiaren planoari buruz zut, hari buruz
zehar samar baizik. Horren ondorioz :- Aurrealdeko planoaren gainean, edo proiekzioaren norabideari buruz
zuta den planoarenean, dauden distantziak eta angeluak eskalan irudikatutzen
dira, eta plano horretan angeluak gorde egiten dira.- Proiekzioaren norabidean distantziak eta angeluak biak aldatzen dira,
baina paraleloek paralelo jarraitzen dute, eta distantzia guztiak berdin txikitzen
dira ; zuzenki baten erdiko puntuak segmentu horren erdiko puntua
ordezkatzen du, edo, norabide horretan peperean distantzia bikoitza dena,
distantzia bikoitza da errealitatean ere.Beste kontu bat da marrazkia ez izatea geometrian lagungarri soil bat baizik,
eta, horregatik, irudi geometrikoen irudikatzea ez da behar bezala zaintzen,
eta gutxi gorabeherako obaloak marrazten dira zirkuluak irudikatu nahi
direnean, edo eskalaren zehaztasunaz arduratu gabe egiten dira marrazkiak.Gauzak, bistan da, ez dira horrela geometria deskribatzailea lantzerakoan,
gauzaki gotorra planoan irudikatzea eta perspektibaren problema aztertzea
baitu helburu geometria mota horrek.
Cavalieriren perspektiban proiekzioa norabide baten arabera egiten da,
baina norabide hori ez dago marrazkiaren planoari buruz zut, hari buruz
zehar samar baizik. Horren ondorioz :- Aurrealdeko planoaren gainean, edo proiekzioaren norabideari buruz
zuta den planoarenean, dauden distantziak eta angeluak eskalan irudikatutzen
dira, eta plano horretan angeluak gorde egiten dira.- Proiekzioaren norabidean distantziak eta angeluak biak aldatzen dira,
baina paraleloek paralelo jarraitzen dute, eta distantzia guztiak berdin txikitzen
dira ; zuzenki baten erdiko puntuak segmentu horren erdiko puntua
ordezkatzen du, edo, norabide horretan peperean distantzia bikoitza dena,
distantzia bikoitza da errealitatean ere.Beste kontu bat da marrazkia ez izatea geometrian lagungarri soil bat baizik,
eta, horregatik, irudi geometrikoen irudikatzea ez da behar bezala zaintzen,
eta gutxi gorabeherako obaloak marrazten dira zirkuluak irudikatu nahi
direnean, edo eskalaren zehaztasunaz arduratu gabe egiten dira marrazkiak.Gauzak, bistan da, ez dira horrela geometria deskribatzailea lantzerakoan,
gauzaki gotorra planoan irudikatzea eta perspektibaren problema aztertzea
baitu helburu geometria mota horrek.
VII Bost poliedro erregularrak
Poliedro erregularrak aurpegiak, ertzak eta erpinak berdinak
dituztenei esaten zaie. Alegia, poliedro erregularrak poligono erregular
berdinez daude eratuta, eta berdinak dituzte orobat angelu
diedroak eta angelu poliedroak ere. Espazioko poliedro erregular
horiek planoko poligono erregularren baliokide dira. Baina planoan
poligonoek edozein alde kopuru izan badezakete, espazioan, berriz,
poliedroak bost baizik ez dira : tetraedroa, kuboa, oktaedroa, dodekaedroa
eta ikosaedroa. Hori horrela da, aldeetako angelu guztien
erpinen baturak ezin duelako 360° baino gehiago izan, eta, angelu
poliedrorik izango bada, gutxienez hiru aldek egin behar dute bat
erpin batean.Aurpegiak karratuak baldin badira, 90°ko angelua dutenak, hiru
aurpegi bakarrik elkar daitezke, hexaedroa edo kuboa eratzen dutela,
zeren eta 90 x 4 = 360 baita.Aurpegiak pentagonoak baldin badira, 108°ko angelua dutenak,
hiru aurpegi bakarrik elkar daitezke, zeren eta 108 x 3= 324° baita,
eta dodekaedro bat eratzen da horrela.Hexagonoetan, barneko angelua 120°koa dutenez, hiru hexagonok
gainalde lau bat eratuko lukete.Hauek dira bost poliedroak :Tetraedroa : lau aurpegi ditu, tankeraz triangelu aldekideak direnak,
sei ertz eta lau erpin. Piramide triangeluar erregularra da.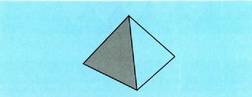 Honela garatzen da :
Honela garatzen da :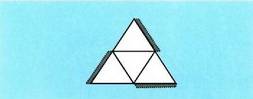 Hexaedroak edo kuboak sei aurpegi ditu, karratuak, hamabi ertz
eta zortzi erpin. Prisma zuzen bat da, oinarritzat karratu bat duena.
Hexaedroak edo kuboak sei aurpegi ditu, karratuak, hamabi ertz
eta zortzi erpin. Prisma zuzen bat da, oinarritzat karratu bat duena.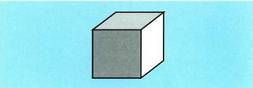 Honela garatzen da :
Honela garatzen da :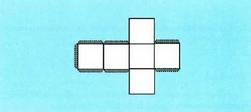 Oktaedroak zortzi aurpegi ditu, triangelu aldekide erakoak,
hamabi ertz eta sei erpin. Karratu itxurako oinetik elkarri itsasita
dauden bi piramideren itxura du.
Oktaedroak zortzi aurpegi ditu, triangelu aldekide erakoak,
hamabi ertz eta sei erpin. Karratu itxurako oinetik elkarri itsasita
dauden bi piramideren itxura du.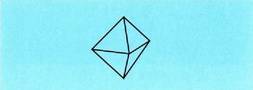 Honela garatzen da :
Honela garatzen da :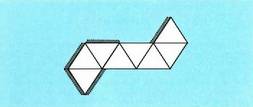 Dodekaedroak hamabi aurpegi ditu, pentagono erregularrak,
hogeita hamar ertz eta hogei erpin.
Dodekaedroak hamabi aurpegi ditu, pentagono erregularrak,
hogeita hamar ertz eta hogei erpin.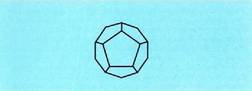 Honela garatzen da :
Honela garatzen da :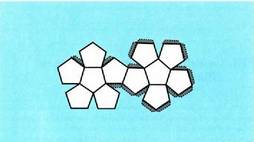 Ikosaedroak hogei aurpegi ditu, triangelu aldekideak, hogeitahamar ertz eta hamabi erpin.
Ikosaedroak hogei aurpegi ditu, triangelu aldekideak, hogeitahamar ertz eta hamabi erpin.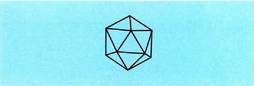 Honela garatzen da :
Honela garatzen da :
Gorputz gotor erregularrak edo platonikoak
Bost gorputz gotor erregularrei gorputz gotor platonikoak esaten zaie,
Platonentzat horiek irudikatzen zituztelako mundua eratzen zuten elementu
soilenak. Hauek dira elementu soil horiek : lurra, ura, airea eta sua ;
eta gorputz guztiek elementu horiek zituzten oinarrian. Elementu horiek
Platonek poliedro erregularrekin egokitu zituen, bakoitzaren mugikortasunaren
arabera. Lurrari, hura baita mugitzen zailena, kuboa egokitu zion ;
urari, mugikorragoa baita, ikosaedroa ; aireari, oktaedroa ; eta suari, azkenik,
tetraedroa, harenak baitira erpinik zorrotzenak eta sarkorrenak.
Geratzen zitzaion irudi bakarrari, dodekaedroari, unibertso osoaren irudikatze
bat balitz bezala hartu zuen. Erdi Aroko alkimistentzat, bestalde,
dodekaedroa gauzen muina edo osagairik garbiena zen.Munduaren irudikatze hori gainbeheran etorri zen. Baina matematikaz
baliaturik mundua interpretzatzeko gogoak bere horretan iraun zuen.
XVII. mendearen hasieran, Alemaniako enperadorearen astronomo Johanes
Keplerrek (1571-1639) planeten orbiten azalpen bat proposatu zuen,
bost poliedro erregularretan oinarritua. Garai hartan sei planeta ezagutzen
ziren : Merkurio, Artizarra, Lurra, Marte, Jupiter eta Saturno. Kepler
Kopernikoren teorien alde zegoen, hau da, uste zuen planeta guztiak eguzkiaren
inguruan biraka ari direla, baina planetak nola zeuden kokatuta eta
zergatik zeuden hala kokatuta esplikatuko zuen teoriarik ez zegoen garai
hartan. Gehienen ustean, planetak esferen gainean zeuden, esfera baitzen
zeruaren irudia, eta esfera horiek orbita zirkularrak egiten zituzten orobat.
Keplerrek planetak bost gorputz gotor platonikoen arabera kokatzea proposatu
zuen. Baina, horretarako, zeruko irudiek esferak behar zuten izan,
eta berak sei planeta kokatu behar zituen eta ez zituen bost gorputz baizik.
Horri irtenbidea emateko, proposatu zuen merkurio oktaedro batean inskribaturiko
esfera baten gainean kokatzea, Artizarra zeukan esfera oktaedro
horretan zirkunskribatua zegoela. Ikosaedroa zetorren gero, eta beste esfera
bat, Lurra barnean zeukana ; dodekaedroa, ondoren, eta beste esfera bat,
Marte zeukana; tetraedroa, eta beste esfera bat, Jupiter zeukana ; eta, azkenik,
kuboa eta beste esfera bat, Saturno zeukana. Esfera guztiak poliedro
batean inskribatuak eta hurrengo poliedroan zirkunskribatuak zeuden.Zoritxarrez, Keplerren irakasle Tycho Brahek planeten mugimenduari
buruz egin zituen neurketak ez zetozen guztiz bat munduaren ikuspegi
horrekin. Horregatik, Keplerrek teoria hori baztertu eta orbita eliptikoak
eta planeten mugimenduaren legeak proposatu zituen, gaur egun ere
Keplerren lege gisa ikasten direnak.
Keplerren irudia.
VIII. Gainalde eta gorputz kurbatuak.
Zilindroa eta konoa.
Irudi bat mugatzen duten gainaldeak gainalde kurboak izan daitezke, aldez edo osoro. Gainalde kurboek mugaturiko gorputzen artean soilenak ardatz baten inguruan lerro bat biratzetik eratzen direnak dira. Segidan aztertuko dira zuzen bat biraraziz eratzen direnak, zilindroak edo konoak, eta zirkunferentzia bat biraraziz eratzen direnak, esferak.
Zilindroak
Zuzen baten inguruan zuzen horren zuzen paralelo bat biraraztean
sortzen den gainaldeari gainalde zilindrikoa esaten zaio.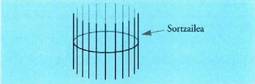 Zuzen nagusiari ardatza esaten zaio, eta birarazten den zuzenari,
berriz, zilindroaren sortzaile.Gainalde zilindriko bat bi zuzen paraleloz ebakitzen bada, zilindro
bat eratzen da.
Zuzen nagusiari ardatza esaten zaio, eta birarazten den zuzenari,
berriz, zilindroaren sortzaile.Gainalde zilindriko bat bi zuzen paraleloz ebakitzen bada, zilindro
bat eratzen da.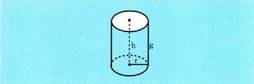 Alboan dauden zuzenak oinarriari buruz zutak badira, zilindroa
zuzena izango da; zutak ez badira, zilindroa zeiharra izango da.Zilindro zuzen bat honela garatzen da :
Alboan dauden zuzenak oinarriari buruz zutak badira, zilindroa
zuzena izango da; zutak ez badira, zilindroa zeiharra izango da.Zilindro zuzen bat honela garatzen da :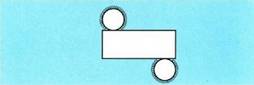 Zilindro zuzenen oinarriak zirkuluak dira ; zilindro zeiharrenak,
berriz, elipseak.Zilindroaren altuera oinarrien arteko distantziari esaten zaio.Zilindro zuzenak laukizuzen bat bere aldeetako baten inguruan
biraraziz ere era daitezke.Zilindro zuzen baten oinarrien arteko zuzen sortzailea bat dator
altuerarekin. Zilindro zuzen baten garrantzi handiko beste datu batzuek
zentroa eta oinarriaren erradioa dira.
Zilindro zuzenen oinarriak zirkuluak dira ; zilindro zeiharrenak,
berriz, elipseak.Zilindroaren altuera oinarrien arteko distantziari esaten zaio.Zilindro zuzenak laukizuzen bat bere aldeetako baten inguruan
biraraziz ere era daitezke.Zilindro zuzen baten oinarrien arteko zuzen sortzailea bat dator
altuerarekin. Zilindro zuzen baten garrantzi handiko beste datu batzuek
zentroa eta oinarriaren erradioa dira.
Konoak
Gainalde konikoa : zuzen bat zuzen horrekiko ebakitzaile den
beste zuzen baten inguruan birarariz sortzen dena da. Zuzen ebakitzaile
hori ardatza da, eta birarazten den zuzena, berriz, gainalde
konikoaren sortzailea.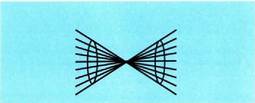 Horrela bi adar sortzen dira, ardatzak eta sortzaileak elkar ebakitzen
duten puntuaren gainetik bata, eta azpitik, bestea ; ebakitze
puntu horri erpina esaten zaio.Gainalde konikoetan garrantzi handia du ardatzak eta sortzaileak eratzen duten angelua
Horrela bi adar sortzen dira, ardatzak eta sortzaileak elkar ebakitzen
duten puntuaren gainetik bata, eta azpitik, bestea ; ebakitze
puntu horri erpina esaten zaio.Gainalde konikoetan garrantzi handia du ardatzak eta sortzaileak eratzen duten angelua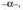 , gainalde koniko hori irekiagoa edo itxiagoa izango den angelu horrek mugatzen baitu.Plano batek gainalde koniko bat ebakitzen badu, zer angelu osatzen
duten, hartara eratuko da :- zirkunferentzia bat, baldin eta planoa elkarzut bada ardatzarekiko.
, gainalde koniko hori irekiagoa edo itxiagoa izango den angelu horrek mugatzen baitu.Plano batek gainalde koniko bat ebakitzen badu, zer angelu osatzen
duten, hartara eratuko da :- zirkunferentzia bat, baldin eta planoa elkarzut bada ardatzarekiko.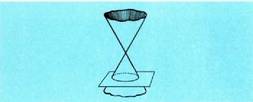 - Baldin eta planoak
- Baldin eta planoak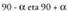 angelua eratzen badu ardatzarekin, lerroa elipse bat izango da.
angelua eratzen badu ardatzarekin, lerroa elipse bat izango da.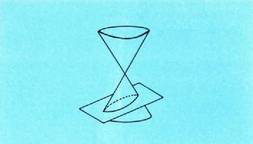 - Baldin eta angelua zehazki
- Baldin eta angelua zehazki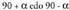 bada, parabola bat eratuko du.
bada, parabola bat eratuko du.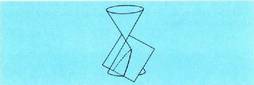 - Baldin eta angelua
- Baldin eta angelua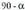 baino txikiagoa edo
baino txikiagoa edo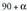 baino handiagoa bada, lerro hori hiperbola bat izango da.
baino handiagoa bada, lerro hori hiperbola bat izango da. Baldin eta gainalde koniko bat ardatzari buruz zuta den plano
batek edo lerro itxi bat eratzeko moduko inklinazioa duen plano
batek ebakitzen badu,.eta gainalde konikoak, erpinak eta planoak
mugaturiko gorputza hartzen bada, kono bat eratzen da. Baldin eta
plano hori ardatzari buruz zuta bada, konoa zuzena izango da ; zuta
ez bada, berriz, konoa zeiharra izango da.
Baldin eta gainalde koniko bat ardatzari buruz zuta den plano
batek edo lerro itxi bat eratzeko moduko inklinazioa duen plano
batek ebakitzen badu,.eta gainalde konikoak, erpinak eta planoak
mugaturiko gorputza hartzen bada, kono bat eratzen da. Baldin eta
plano hori ardatzari buruz zuta bada, konoa zuzena izango da ; zuta
ez bada, berriz, konoa zeiharra izango da.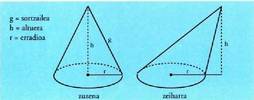 Erpinaren eta konoaren oinarriaren arteko distantziari konoaren
altuera esaten zaio. Konoa zuzena bada, oinarria zirkulu bat izango
da, eta zirkulu horren erradioa zein den jakin beharko da. Kono
zuzenetan, erpina oinarriaren gainean proiektatuz gero, proiekzio
hori haren zentro-zentroan egongo da.Kono zuzena honela garatzen da :
Erpinaren eta konoaren oinarriaren arteko distantziari konoaren
altuera esaten zaio. Konoa zuzena bada, oinarria zirkulu bat izango
da, eta zirkulu horren erradioa zein den jakin beharko da. Kono
zuzenetan, erpina oinarriaren gainean proiektatuz gero, proiekzio
hori haren zentro-zentroan egongo da.Kono zuzena honela garatzen da :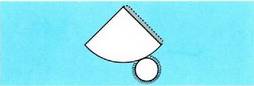 Baldin eta kono bat oinarriko planoari buruz paraleloa den beste
plano batek ebakitzen badu, horrela eratzen den irudiari kono
enborra esaten zaio.
Baldin eta kono bat oinarriko planoari buruz paraleloa den beste
plano batek ebakitzen badu, horrela eratzen den irudiari kono
enborra esaten zaio.
- Ariketak
10. Zer motatako epaiak era daitezke plano batek zilindro bat ebakitzen duenean?11. Inurri bat pote zilindriko baten alboko gainaldearen altuera erdian dago. Goiko ertzean dagoen marmelada tanta batera heldu nahi du. Baldin eta ertzari buruz perpendikular igotzen bada, 8 cm. ibili beharko ditu gora iritsi arte, eta, gero, beste 6 cm. egin beharko ditu jatekora iritsi arte. Zein du inurriak bide zuzenena, eta zer luzera du bide horrek? (Erabili zilindroaren garapena).
IX. Esfera
Esfera : zirkunferentziaerdi bat bere diametroaren inguruan biraraziz
eratzen den gainaldea.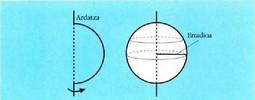 Esfera beste modu batera ere defini daiteke : zentroa deitzen den
puntu finko batetik distantzia berera dauden espazioko puntuen
leku geometrikoa. Distantzia finko horri erradioa esaten zaio. Zentrotik
pasa eta esferako bi puntu lotzen dituzten zuzenkiei diametroak
esaten zaie, eta diametro horien luzera bi aldiz erradioa da.
Esfera beste modu batera ere defini daiteke : zentroa deitzen den
puntu finko batetik distantzia berera dauden espazioko puntuen
leku geometrikoa. Distantzia finko horri erradioa esaten zaio. Zentrotik
pasa eta esferako bi puntu lotzen dituzten zuzenkiei diametroak
esaten zaie, eta diametro horien luzera bi aldiz erradioa da.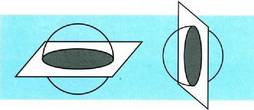 Baldin eta zentrotik igarotzen ez den plano batek esfera ebakitzen
badu, oinarri bereko bi segmentu esferiko egingo ditu. Esferan eratzen
duen gainaldeari txapel esferikoa esaten zaio.
Baldin eta zentrotik igarotzen ez den plano batek esfera ebakitzen
badu, oinarri bereko bi segmentu esferiko egingo ditu. Esferan eratzen
duen gainaldeari txapel esferikoa esaten zaio.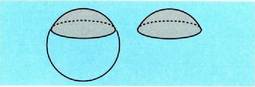 Bi plano paralelok esfera bat ebaki badute, bi oinarriko segmentu
esferiko bat eratzen dute. Horien gainaldeari gune esferikoa esaten zaio.
Bi plano paralelok esfera bat ebaki badute, bi oinarriko segmentu
esferiko bat eratzen dute. Horien gainaldeari gune esferikoa esaten zaio. Baldin eta bi plano horiek diametro batean elkar ebakitzen badute,
horrela eratzen den irudiari ziri esferikoa esaten zaio.
Baldin eta bi plano horiek diametro batean elkar ebakitzen badute,
horrela eratzen den irudiari ziri esferikoa esaten zaio.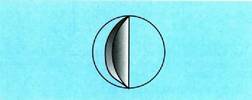 Puntu batetik esferaren zentrorainoko distantzia esferaren erradioa
baino txikiagoa, berdina ala handiagoa izan, hala dago puntu
hura esfera barnean, haren gainaldean ala esferaz kanpo.
Puntu batetik esferaren zentrorainoko distantzia esferaren erradioa
baino txikiagoa, berdina ala handiagoa izan, hala dago puntu
hura esfera barnean, haren gainaldean ala esferaz kanpo.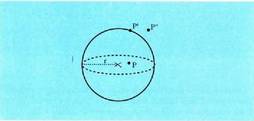 Era berean, zuzen batetik esferaren zentrorainoko distantzia erradioa
baino txikiagoa, berdina ala handiagoa izan, hala da zuzen hura
esferaren ebakitzaile, ukitzaile ala esferaz kanpoko.Zuzen batek bi puntutan ebakitzen du esferaren gainaldea. Zuzen
horretatik zentrora dagoen distantzia zero baldin bada, bi puntu
horiek diametro baten muturrak dira.
Era berean, zuzen batetik esferaren zentrorainoko distantzia erradioa
baino txikiagoa, berdina ala handiagoa izan, hala da zuzen hura
esferaren ebakitzaile, ukitzaile ala esferaz kanpoko.Zuzen batek bi puntutan ebakitzen du esferaren gainaldea. Zuzen
horretatik zentrora dagoen distantzia zero baldin bada, bi puntu
horiek diametro baten muturrak dira.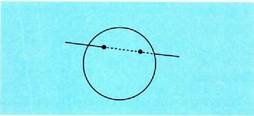 Ukitzailea ukitze puntura doan erradioarekiko elkarzuta da. Esfera
baten puntutik zuzen ebakitzaile kopuru infinitoa marraz daiteke.
Ukitzailea ukitze puntura doan erradioarekiko elkarzuta da. Esfera
baten puntutik zuzen ebakitzaile kopuru infinitoa marraz daiteke.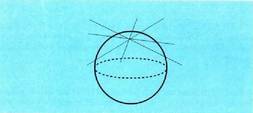 Plano batetik esferaren zentrorainoko distantzia esferaren erradioa
baino txikiagoa, berdina ala handiagoa izan, hala da plano hori
esferaren ebakitzaile, ukitzaile ala esferaz kanpoko.Plano batek zirkulu baten arabera ebakitzen du esfera, eta plano
horrekiko diametro perpendikularra zirkulu horren zentrotik igarotzen
da.
Plano batetik esferaren zentrorainoko distantzia esferaren erradioa
baino txikiagoa, berdina ala handiagoa izan, hala da plano hori
esferaren ebakitzaile, ukitzaile ala esferaz kanpoko.Plano batek zirkulu baten arabera ebakitzen du esfera, eta plano
horrekiko diametro perpendikularra zirkulu horren zentrotik igarotzen
da.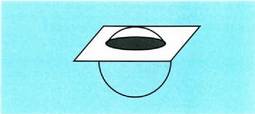 Ukitze puntura doan erradioa perpendikularra da plano ukitzaileari
buruz. Esfera bateko puntu batetik plano ukitzaile bakarra
dago, eta zuzen ukitzaile guztiak plano horren barnean dira.
Ukitze puntura doan erradioa perpendikularra da plano ukitzaileari
buruz. Esfera bateko puntu batetik plano ukitzaile bakarra
dago, eta zuzen ukitzaile guztiak plano horren barnean dira.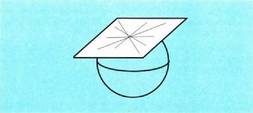 Bi esferen zentroen arteko distantzia erradioen batura baino handiagoa,
berdina ala txikiagoa izan, hala dira bi esfera haiek kanpoko,
ukitzaile eta kanpoko, ebakitzaile, ebakitzaile eta barneko, ukitzaile
eta barneko edo barneko. Eta distantzia erradioen batura baino txikiagoa
baldin bada, hiru gauza gerta daitezke : a) zentroen arteko
distantzia erradioen arteko diferentzia baino handiagoa izatea, eta
orduan esferek elkar ebakitzen dute ; b) zentroen arteko distantzia
eta erradioen arteko diferentzia berdinak izatea, eta orduan esfera
bat bestearen barne ukitzailea da; c) zentroen arteko distantzia erradioen
arteko diferentzia baino txikiagoa izatea, eta orduan esfera bat
bestearen barnean dago. Zentroen arteko distantzia zero denean, bi
esfera horiek kontzentrikoak dira.
Bi esferen zentroen arteko distantzia erradioen batura baino handiagoa,
berdina ala txikiagoa izan, hala dira bi esfera haiek kanpoko,
ukitzaile eta kanpoko, ebakitzaile, ebakitzaile eta barneko, ukitzaile
eta barneko edo barneko. Eta distantzia erradioen batura baino txikiagoa
baldin bada, hiru gauza gerta daitezke : a) zentroen arteko
distantzia erradioen arteko diferentzia baino handiagoa izatea, eta
orduan esferek elkar ebakitzen dute ; b) zentroen arteko distantzia
eta erradioen arteko diferentzia berdinak izatea, eta orduan esfera
bat bestearen barne ukitzailea da; c) zentroen arteko distantzia erradioen
arteko diferentzia baino txikiagoa izatea, eta orduan esfera bat
bestearen barnean dago. Zentroen arteko distantzia zero denean, bi
esfera horiek kontzentrikoak dira.
Ebazpenak
1. AB 11 EF 11 HG 11 DC ; AB gurutzatzen da EH, FG , HD eta
GC-rekin.ABk ebakitzen ditu EA, DA, BC eta BF2. a) ABCDk ebakitzen ditu ABEF, BCFG, HGDC, eta ADHE.b) ABCD 11 EFGH3. AB, CD, EF eta HG ertzak erditik ebakitzen dituena da plano
erdibitzailea. ABCD edo ABEF aurpegia mugatzen duten zuzenkiak
erdiko puntuan dagoen zuzen perpendikular baten barnean
egongo dira.4. ADEHri buruz zuta den eta Atik eta Htik pasatzen den planoa
bakarra da eta Gtik eta Btik pasatzen da. AHM mugatzen duen planoa
ere bakarra da, eta ADEHri buruz zuta baldin bada, bat dator
aurreko planoarekin ; baina B eta G barnean dituen zuzen baten arabera
ebakitzen du BFGC planoa, beraz Mk ere zuzen horretan egon
behar du; hala, B, G eta M lerrokatuta daude.5. Dtik eta Mtik pasatzen den zuzenean, zuzen baten arabera
ebakitzen dutelako elkar, eta bi puntuk zuzen bat mugatzen dutelako
.6. Hartzen badugu A erpina, B, D eta Era dagoen distantzia 2 banakokoa da, C, F eta Hra dagoena,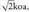 , eta G aurkako erpinera dagoena, berriz,
, eta G aurkako erpinera dagoena, berriz,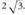 7. Demagun M dela AB ertzaren erdiko puntua. d(MA) _
d(MB) = 1.d(MC) = d(MD) = d(MF) = d(ME) = V(5)d(MG) = d(MH) = 38. Oinarria lauki bat duen piramidea : 8 ertz, 5 erpin eta 5 alde.
7. Demagun M dela AB ertzaren erdiko puntua. d(MA) _
d(MB) = 1.d(MC) = d(MD) = d(MF) = d(ME) = V(5)d(MG) = d(MH) = 38. Oinarria lauki bat duen piramidea : 8 ertz, 5 erpin eta 5 alde.
5+5= 8+2Piramide hexagonal baten gerria : 18 ertz, 12 erpin eta 8 aurpegi
12+8 = 18 + 29. Oinarria 3 cm.ko aldea duen triangelua da, eta aldeak triangelu isosezleak dira, oinarrian 3 dutenak eta aldeak luzera berekoak dituztenak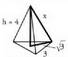 3
10. Baldin eta ardatzari buruz zuta bada, zirkulua : baldin
eta zeiharra bada, elipsea ; eta baldin eta ardatza barnean
badu, bi zuzen
3
10. Baldin eta ardatzari buruz zuta bada, zirkulua : baldin
eta zeiharra bada, elipsea ; eta baldin eta ardatza barnean
badu, bi zuzen