Fisika-Kimika»Fisika - Kimika
Zinematika
2. Puntuaren zinematika
2.1. Sarrera
Mekanikak gorputzen mugimendua eta mugimendu horiek sortzen dituzten indarrak aztertzen ditu. Definizio horren bi alderdien arabera, hiru alorretan banatzen da mekanika: zinematika edo mugimenduaren teoria geometrikoa, estatika edo indarren teoria, eta dinamika edo indarren eta indarrek sortzen dituzten mugimenduen arteko harremanen azterketa.
Atal honetan zinematika aztertuko da. Lehenengo jakingaia gorputz soil eta oinarrizkoena aztertzea da, gorpuzki puntua edo gor - puzkia, alegia; gorpuzki puntua esaten zaio haren mugimendua aztertzerakoan haren dimentsioak kontuan hartzekoak ez diren gorputzari. Ebatzi beharreko problema bakoitzaren baldintza berezien arabera erabakiko da gorputz jakin baten dimentsioak kontuan hartu beharrekoak diren ala ez. Adibidez, planetak gorpuzki puntutzat har daitezke Eguzkiaren inguruan egiten dituzten mugimenduak aztertu nahi direnean, baina ezin dira gorpuzki puntutzat hartu planeta horiek beren ardatzen inguruan egunero egiten duten errotazioa aztertu nahi denean.
Gorpuzki puntu baten mugimendua deskribatzeko, erreferentzia sistema esaten zaion hiru ardatz lauki zuzeneko sistema bat hartu behar da. Puntu bat erreferentzia sistema bati buruz geldi dago, sistema horretako puntu guztiekiko distantziak konstanteak dituenean. Distantzia horiek aldatzen direnean, puntu hori mugitzen ari da sistema horri buruz.
Puntua mugitzen denean posizio batetik bestera igarotzen da. Gertaera horrek iraupen jakin bat du, eta bitarte jakin bat behar izaten du. Puntua, beraz, tarteko posizio guztietatik igarotzen da bitarte jakin batzuetan, eta puntuari dagokion posizioak definitzen du une bakoitza. Muturreko uneak, alegia bitarte horretako hasierako unea eta bukaerako unea, puntu horren hasierako eta bukaerako posizioei dagozkie. Hasierako unea hasierako posizioari baldin badagokio, orduan azkeneko unea azkeneko posizioarekin batera aldatuko da. Denbora bitartearen magnitudea aldatu egiten da, eta aldagai eskalar bat du neurri, t, denbora esaten zaiona. Bitarte jakin baten azkeneko unea t denboraren balioak definitzen du, eta t unea esaten zaio. Mekanikaren alorrean, t aldagaia aldagai independentetzat hartzen da ia beti, eta berez du gehitzeko joera. Gainera, denbora unibertsala da; modu berean igarotzen da erreferentzia sistema guztietan.
2.2. Luzera eta denbora unitateak
Zinematikan behar diren magnitude guztiak definitzeko, aski da oinarri-oinarrizko bi unitate aukeratzea, luzera unitatea eta denbora unitatea.
Metroa (m) da luzeraren unitatea. Nazioarteko Unitate Sistemaren arabera (SI du laburdura), 86 Kr isotopoak 2p10 eta 5d5. mailen arteko trantsizioan igortzen duen irradaren 1 650 763,73 uhin luzeren berdina da metroa.
Segundua (s) 1900eko tropiko urtearen iraupenaren 1/31556925,975 zatia da.
LASTERTASUNA ETA AZELERAZIOA
2.3. Puntu baten mugimendua
P gorpuzki materialak espazioan duen posizioa O puntu finkotik P puntura dihoan posizio bektoreak definitzen du. O puntutik sortzen diren koordenatu lauki zuzenen sisteman, P puntuaren (x,y,z) koordenatuak dira r bektorearen osagaiak (2.1. irudia). P puntua mugitzen bada, C kurba bat eratuko du espazioan; kurba horri, definizioz, P puntuaren ibilbidea esaten zaio.
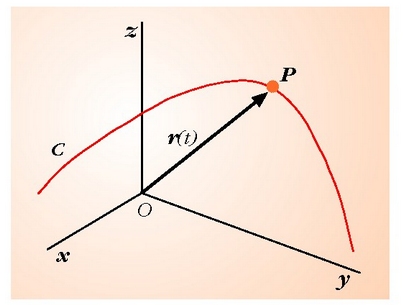
2.1. irudia. r posizio bektoreak definitzen du edozein unetan Oxyz erreferentzia sistemari buruz mugitzen ari den P puntuaren posizioa
a) P puntuaren mugimendua erabat definitzen da hiru koordenatuek denboraren arabera dituzten balioak ezagutuz gero, alegia:
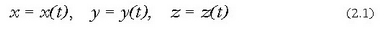
(2.1) ekuazioei ibilbidearen ekuazio parametrikoak esaten zaie. Ekuazio horiek ibilbideko puntu jakin bateko koordenatuak (x,y,z) egokiarazten dizkio t denboraren balio bakoitzari. Ibilbidearen ekuazioa zein den jakiteko, aski da ekuazio parametriko horietatik denbora kentzea.
z=0 kasu berezian, puntu hori xy planoan mugitzen da, eta y=z=0 baldin bada, puntu hori x ardatzaren gainean mugitzen da.
Mugimendu ekuazioak (2.1) ezagutzen direnean,

ekuazio horrek edozein unetan mugatzen du r posizio bektorea. Horregatik esaten da r t denboraren bektore funtzioa dela, eta sinbolo hauez idazten da

Ekuazio horri puntuaren mugimenduaren bektore ekuazioa esaten zaio.
b) Kasu batzuetan, puntu jakin baten mugimendua honela definitzen da: C ibilbidearen gainean P0 puntu finko bat eta noranzko positibo bat hartzen dira modu arbitrarioan (2.2. irudia). s arkuaren luzerak definitzen du, luzera hori algebrako magnitudetzat harturik, P puntu mugikorrak edozein unetan duen posizioa. Beraz, t denboraren balio bakoitzari s arkuaren luzeraren balio bat egokituko zaio, hau da:

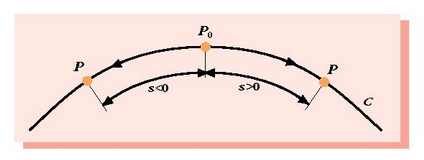
2.2. Irudia. s arkuaren luzerak eta hari dagokion zeinuak mugatzen du, edozein unetan, P puntuaren posizioa
s parametroari berezkoa esaten zaio, eta (2.4) ekuazioari mugimenduaren berezko ekuazioa edo mugimenduaren ekuazioa, besterik gabe, esaten zaio. Ekuazio horren bidez ez dago mugimendua definitzerik, aldez aurretik ez bada puntuaren ibilbidea jakiten.
Oharra: Ez nahastu r = r(t) ekuazioa eta s = s(t) ekuazioak.
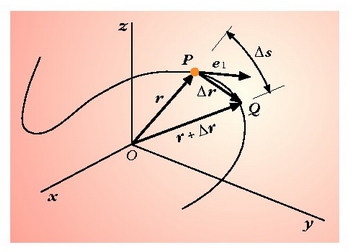
2.3. Irudia. Posizio bektorearen deribatua arkuari buruz unitate bektore bat da, ukitzailearen norabidea eta s gehikuntzaren noranzkoa duena
2.4. Posizio bektorearen deribatua arkuari buruz. Banako bektore ukitzailea
P puntu batek une bakoitzean duen posizioa s arkuaren luzerak edo r erradio bektoreak definitzen dute (2.3. irudia).
Q beste puntu bat hartuz gero, arku horren balioa
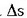 gehitzen da,
eta erradio bektorea, berriz,
gehitzen da,
eta erradio bektorea, berriz, 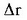 gehitzen da; r erradio bektorea eskalarraren funtzio bat da, alegia. Beraz:
gehitzen da; r erradio bektorea eskalarraren funtzio bat da, alegia. Beraz:
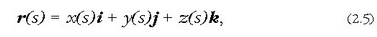
edo bestela:

Baina 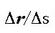 bektore bat denez, eta
bektore bat denez, eta
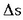 berriz, eskalar bat,
berriz, eskalar bat,
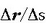 bektoreak
bektoreak
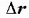 gehikuntzaren norabide eta noranzko berberak ditu.
Limitean,
gehikuntzaren norabide eta noranzko berberak ditu.
Limitean, 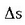 gehikuntzak zerorako joera duenean,
gehikuntzak zerorako joera duenean,
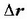 gehikuntzaren norabideak P puntuaren
ibilbidearen ukitzailearekin bat egiteko joera du. Honela idatz daiteke beraz:
gehikuntzaren norabideak P puntuaren
ibilbidearen ukitzailearekin bat egiteko joera du. Honela idatz daiteke beraz:

Beraz, dr/ds bektoreak kurba P puntuan ukitzen duen ukitzailearen norabide bera du, eta PQ bektorearen noranzko bera, s gehikuntzena, alegia. Haren moduluari dagokionez, limitean, As gehikuntzak zerorako joera duenean, PQ lerroaren luzeraren eta PQ arkuaren luzeraren arteko erlazioa banakoa da; alegia,

Beraz:

formula horretan, et unitate bektore bat da, ukitzailearen norabidea du, eta s gehikuntzen noranzkoa.
(2.2) ekuazioak definitzen badu r bektorea, orduan:
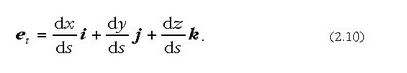
eta
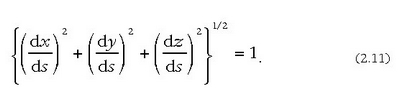
2.5. Posizio bektorearen bigarren deribatua arkuari buruz. Arau nagusia
r posizio bektorearen bigarren deribatua kurbaren arkuarekiko, d 2 r/ ds 2, aztertuko da orain; dr/ds-ren deribatua, alegia. (2.9) ekuaziotik hau ateratzen da:
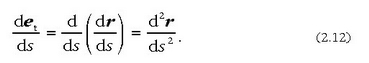
 kalkulatu behar da beraz.
et unitate bektore bat denez, haren deribatua,
kalkulatu behar da beraz.
et unitate bektore bat denez, haren deribatua, 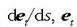 elkarzuta da bektoreari buruz.
elkarzuta da bektoreari buruz. 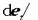 bektorea ondoz
ondoko bi ukitzaileren planoan dago beraz (plano biltzailea); normal nagusiaren norabide bera du (plano biltzailearen baitan dagoen normala),
eta sakonunearen noranzko bera.
bektorea ondoz
ondoko bi ukitzaileren planoan dago beraz (plano biltzailea); normal nagusiaren norabide bera du (plano biltzailearen baitan dagoen normala),
eta sakonunearen noranzko bera.
Bektore horren modulua zein den jakiteko, kurba horretako bi puntu hartu behar dira, P eta Q, s eta s +
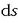 koordenatuak dituztenak.
Demagun et eta et +Det direla puntu horiei dagozkien banako bektore ukitzaileak (2.4. irudia).
Q puntutik et-ren bektore ekipolentea marraztuko da. Plano biltzailean kurbako P eta Q puntuen normalak marraztuko dira.
koordenatuak dituztenak.
Demagun et eta et +Det direla puntu horiei dagozkien banako bektore ukitzaileak (2.4. irudia).
Q puntutik et-ren bektore ekipolentea marraztuko da. Plano biltzailean kurbako P eta Q puntuen normalak marraztuko dira.
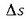 arkuak bat egin dezake erdigunetzat O duen zirkunferentziarekin,
eta erdigune hori da orobat normalek bat egiten duten puntua. Zirkunferentzia horren erradioak,
arkuak bat egin dezake erdigunetzat O duen zirkunferentziarekin,
eta erdigune hori da orobat normalek bat egiten duten puntua. Zirkunferentzia horren erradioak,
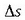 makurdura erradioa du izena. Bi ukitzaileek eratzen duten
makurdura erradioa du izena. Bi ukitzaileek eratzen duten
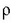 angelua eta OP eta OQ erradioek eratzen dutena berdinak dira.
Beraz, honela idatz daiteke:
angelua eta OP eta OQ erradioek eratzen dutena berdinak dira.
Beraz, honela idatz daiteke:

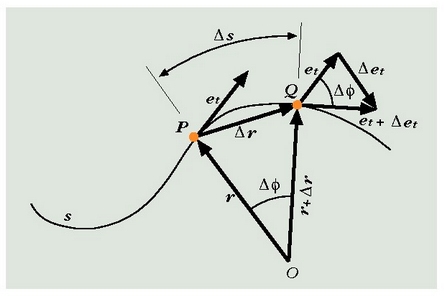
2.4. irudia. Posizio bektorearen bigarren deribatua arkuari buruz 1/r modulua duen eta en unitate bektorearen noranzko bera duen bektore bat da.
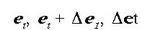 bektoreek eratzen duten triangelua isoszele da, zeren eta
bektoreek eratzen duten triangelua isoszele da, zeren eta
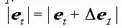 baita. Beraz:
baita. Beraz:
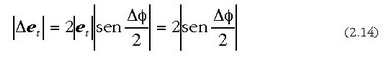
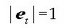 da eta. Berdintza horren bi osagaiak zati
da eta. Berdintza horren bi osagaiak zati
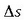 eginez, hau ateratzen da:
eginez, hau ateratzen da:
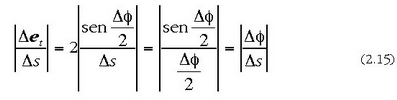
eta hori limitera eramanez, hau ateratzen da:
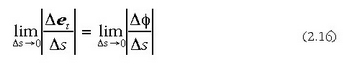
zeren eta 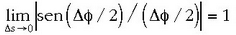 baita. Beraz:
baita. Beraz:

eta, (2.13) kontuan harturik, hau ateratzen da:

alegia, 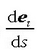 -ren modulua
-ren modulua
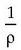 da. Modu horretan, garrantzi handiko ekuazio hau ateratzen da:
da. Modu horretan, garrantzi handiko ekuazio hau ateratzen da:

ekuazio horretan 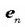 unitate bektore bat da,
arau nagusiaren araberako norabidea duena.
unitate bektore bat da,
arau nagusiaren araberako norabidea duena.
(2.19) formulatik hau ateratzen da:

eta, beraz:
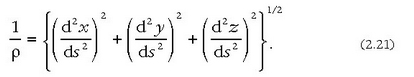
2.6. Lastertasun bektorea
Demagun t denboran puntua P-n dagoela, eta
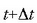 denboran puntua Q-n dagoela.
Definizioz,
denboran puntua Q-n dagoela.
Definizioz, 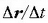 erlazioari puntu horrek
erlazioari puntu horrek
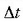 bitartean duen batez besteko lastertasuna esaten zaio.
bitartean duen batez besteko lastertasuna esaten zaio.
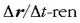 limitearen balioari,
limitearen balioari,
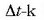 zerorako joera duenean,
uneko lastertasuna esaten zaio. Beraz:
zerorako joera duenean,
uneko lastertasuna esaten zaio. Beraz:
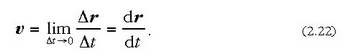
(2.6) ekuazioa denborari buruz deribatuz gero, hau ateratzen da:
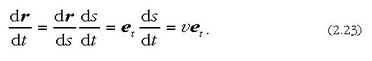
edo bestela:

Beraz, lastertasun bektoreak ibilbidearen ukitzailearen norabide bera du. Aurreko ekuazio horren bi aldeetako balio absolutuak hartuz gero, eta et unitate bektore bat dela kontuan harturik, hau ateratzen da:

alegia, ibilbidean egiten den oinarri-oinarrizko leku aldatzea neurtzen duten zenbakien eta leku aldatze horri dagokion bitartearen arteko erlazioak definitzen du lastertasun bektorearen modulua.
(2.25) ekuazioaren arabera, puntu jakin batek denbora banako bakoitzean luzera unitate bat egiten duenean,
orduan lastertasun unitatea du. Zentimetro/segundotan 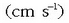 eta metro/segundotan
eta metro/segundotan 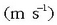 adierazten da.
adierazten da.
2.7. Angelu lastertasuna
xy planoan har dezagun OA zuzen mugikor bat O muturraren inguruan biraka dabilena; mutur hori ez da mugitzen (2.5. irudia). f baldin bada t unean zuzen horrek planoko Ox norabide finkoarekin eratzen duen angelua; f angelu hori denboraren funtzioa da. w bektoreari zuzen horren errotazioaren angelu lastertasuna esaten zaio; bektore horren modulua f-ren deribatua da denborari buruz, alegia:

bektore horrek norabide normala du plano finkoarekiko,
eta noranzkoa, berriz, torloju batek errotazioaren noranzkoan biraka sartzen denean duen noranzko berbera du.
Angelu lastertasuna radian 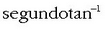 neurtzen da.
neurtzen da.
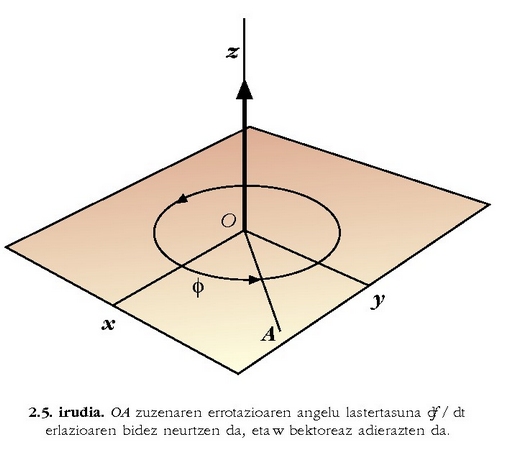
2.5. irudia. OA zuzenaren errotazioaren angelu lastertasuna df / dt erlazioaren bidez neurtzen da, eta w bektoreaz adierazten da.
2.8. Azelerazio bektorea
Kurba mugimenduan lastertasuna aldatu egiten da, oro har, moduluan, norabidean eta noranzkoan.
Baldin eta t unean P puntuaren lastertasuna v baldin bada, eta
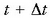 unean, berriz,
unean, berriz,
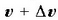 baldin bada haren lastertasuna,
baldin bada haren lastertasuna,
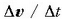 erlazioari puntu horrek
erlazioari puntu horrek
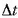 bitartean duen batez besteko lastertasuna esaten zaio (2.6. irudia).
bitartean duen batez besteko lastertasuna esaten zaio (2.6. irudia).
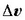 gehikuntzak duen norabide eta noranzko berbera izango du.
gehikuntzak duen norabide eta noranzko berbera izango du.
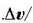
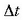 erlazioaren limite balioari,
erlazioaren limite balioari,
 gehikuntzak zerorako joera duenean,
une bateko azelerazioa esaten zaio. Beraz:
gehikuntzak zerorako joera duenean,
une bateko azelerazioa esaten zaio. Beraz:
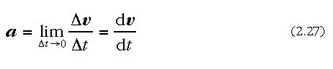
edo bestela, posizio bektorearen arabera:
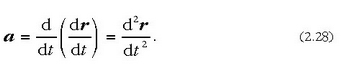
Azelerazio bektorearen norabidea eta noranzkoa aurrerago adieraziko dira.
Azelerazioa cm 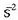 eta m
eta m 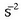 neurritan adierazten da.
neurritan adierazten da.
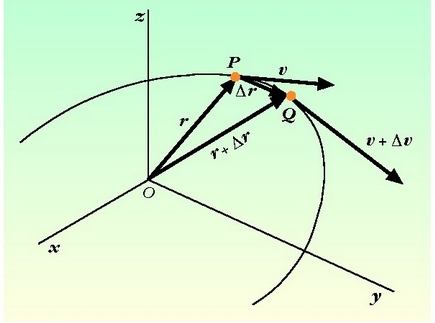
2.6. irudia. Une bateko azelerazioa lastertasun bektorearen lehenengo deribatuaren berdina da, edo puntu jakin baten erradioa den bektor earen bigarren deribatuaren berdina denborari buruz
2.9 Lastertasunaren eta azelerazioaren laukizuzeneko osagaiak
r bektoreak edozein unetan duen posizioa (2.2) ekuazioak mugatzen baldin badu, orduan, i, j, k unitate bektoreak konstanteak direla kontuan harturik, hau ateratzen da:
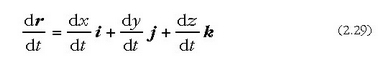
eta
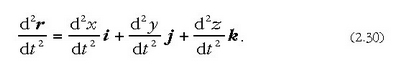
Beraz, hauek izango dira lastertasun bektorearen eta azelerazio bektorearen osagaiak, koordenatuen ardatzen arabera:
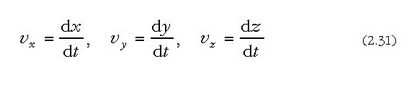
eta
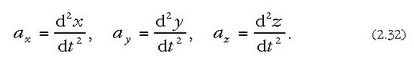
alegia, v eta a-ren lauki zuzeneko osagaiak koordenatuen lehenengo eta bigarren deribatuak dira denborari buruz.
Lastertasunaren eta azelerazioaren balio absolutua era honetara adierazten da:
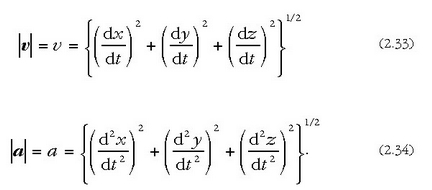
2.10 Azelerazioak berez dituen osagaiak
Puntu baten azelerazioa zein den jakiteko, (2.24) ekuazioa deribatu behar da denborari buruz. Hau ateratzen da:
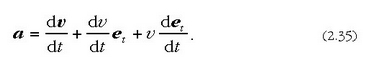
Baina kurban zehar et s arkuaren funtzioa da, zeren eta haren moduluak konstante irauten badu ere, haren norabidea eta noranzkoa aldatu egiten baitira. Beraz, era honetara adieraz daiteke:
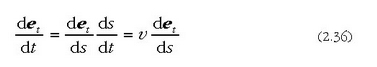
(2.35) ekuazioan, 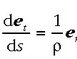 dela kontuan harturik, elementu hori ordezkatzen badugu, hau ateratzen da azkenik:
dela kontuan harturik, elementu hori ordezkatzen badugu, hau ateratzen da azkenik:
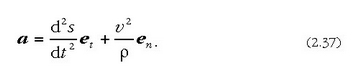
Azelerazioa, beraz, plano biltzailean dagoen bektore bat da, eta plano horrek
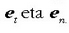 dauzka bere baitan.
dauzka bere baitan.

bektoreen arteko biderkadura horrek triedro zuzen bat eratzen du,
eta hirugarren bektore bat definitzen du et eta 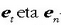 -ri
buruz elkarzuta
dena. Puntutik
-ri
buruz elkarzuta
dena. Puntutik 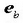 norabidean igarotzen den lerro zuzenari kurbaren
binormala P puntuan esaten zaio.
norabidean igarotzen den lerro zuzenari kurbaren
binormala P puntuan esaten zaio. 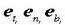 bektoreari unitate bektore
binormala esaten zaio. et, en, eb, unitate bektoreek, ordena horretan
hartuta, eratzen duten triedroari berezko triedroa edo Freneten
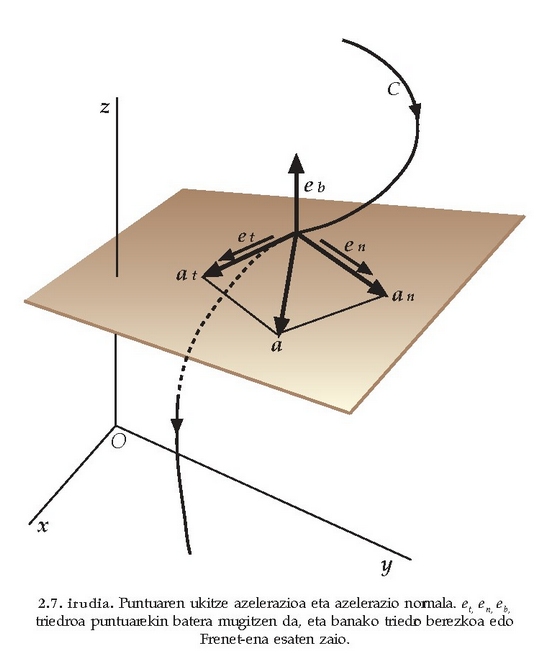
triedroa esaten zaio (2.7. irudia).
bektoreari unitate bektore
binormala esaten zaio. et, en, eb, unitate bektoreek, ordena horretan
hartuta, eratzen duten triedroari berezko triedroa edo Freneten
triedroa esaten zaio (2.7. irudia).
Beraz, v lastertasun bektoreak ukitze azelerazioa duen bitartean,
a azelerazio bektorea bi osagai elkarzutetan deskonposa daiteke:
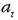 osagaia,
ibilbidearen ukitzailearekin bat egiten duena, eta ukitze azelerazioa esaten zaiona, eta
osagaia,
ibilbidearen ukitzailearekin bat egiten duena, eta ukitze azelerazioa esaten zaiona, eta
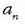 osagaia, normalarekin bat egiten duena,
azelerazio normala esaten zaiona.
osagaia, normalarekin bat egiten duena,
azelerazio normala esaten zaiona.
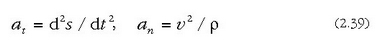
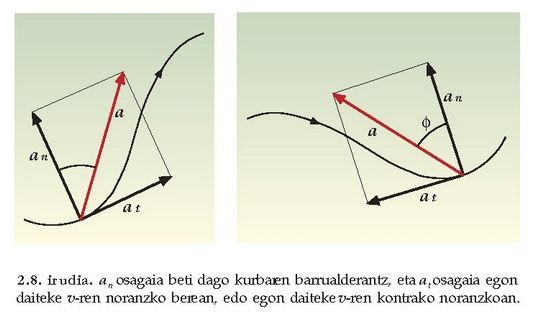
a1 ukitze azelerazioa positiboa izango da vren noranzko berean baldin badago,
eta negatiboa, berriz, v-ren kontrako noranzkoan baldin badago. Azelerazio normala,
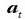 positiboa da beti, kurbaren barrualderantz egiten baitu beti, eta, arrazoi horregatik,
azelerazio zentripetoa esaten zaio (2.8 irudia).
positiboa da beti, kurbaren barrualderantz egiten baitu beti, eta, arrazoi horregatik,
azelerazio zentripetoa esaten zaio (2.8 irudia).
a azelerazio bektorearen modulua hau da:

eta bektore horrek normalarekin eratzen duen f angelua era honetara adierazten da:

MUGIMENDU MOTA BATZUEN EZTABAIDA
2.11 Mugimendu uniformea
Lastertasun konstantea duen mugimenduari mugimendu uniformea esaten zaio. (2.22) ekuaziotik ondorio hau ateratzen da:
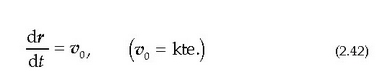
edo bestela:

Integrala eginez, hau ateratzen da:

alegia,

ekuazio horretan 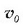 eta
eta 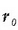 (integraziozko konstantea) bektore konstanteak dira.
Beraz, 2.9 iruditik ateratzen den ondorioaren arabera, ibilbide hori lerro zuzen bat da;
zenbaki lastertasun konstantea du
(integraziozko konstantea) bektore konstanteak dira.
Beraz, 2.9 iruditik ateratzen den ondorioaren arabera, ibilbide hori lerro zuzen bat da;
zenbaki lastertasun konstantea du 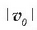 ,
eta
,
eta 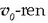 norabide eta noranzko bera ditu.
norabide eta noranzko bera ditu. 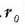 bektoreak P puntuaren erradio bektorea irudikatzen du t=0 denean.
bektoreak P puntuaren erradio bektorea irudikatzen du t=0 denean.
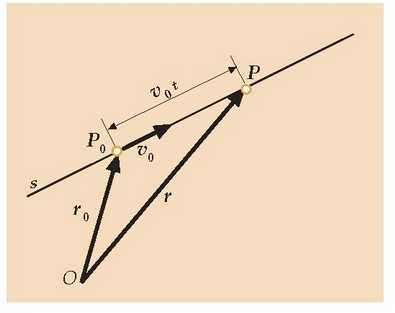
2.9. irudia. Puntu baten lastertasun bektorea konstantea baldin bada, bektore horren mugimendua zuzena eta uniformea izango da.
2.12 Azelerazio uniformea duen mugimendua
Azelerazio bektorea konstantea duen mugimenduari azelerazio uniformea duen mugimendua esaten zaio. (2.27) ekuaziotik ondorio hau ateratzen da:
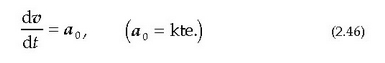
edo bestela:

Integrala eginez, hau ateratzen da:

alegia,

ekuazio horretan 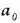 eta
eta 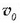 (integraziozko konstantea) bektore konstanteak dira. Baina aurreko ekuazio horren ordez (2.22) ekuazioa jartzen bada, hau ateratzen da:
(integraziozko konstantea) bektore konstanteak dira. Baina aurreko ekuazio horren ordez (2.22) ekuazioa jartzen bada, hau ateratzen da:
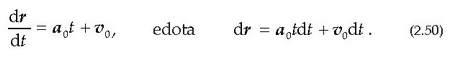 Integrala eginez, hau ateratzen da:
Integrala eginez, hau ateratzen da:
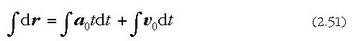
alegia,
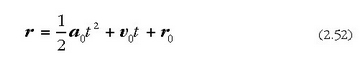
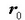 bektoreak P puntuaren posizio bektorea irudikatzen du, aurreko kasuan bezala, t=0 denean;
bektoreak P puntuaren posizio bektorea irudikatzen du, aurreko kasuan bezala, t=0 denean;
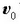 bektoreak, berriz, hasierako lastertasuna irudikatzen du.
bektoreak, berriz, hasierako lastertasuna irudikatzen du.
(2.52) ekuazioaren arabera, 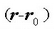 bektorea
bektorea 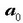 eta
eta  bektoreen konbinazio linealaz ateratzen da.
Beraz, bektore hori
bektoreen konbinazio linealaz ateratzen da.
Beraz, bektore hori 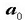 eta
eta 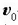 -k definitutako planoan egoten da beti.
Bektore horren ibilbidea kurba lau bat izaten da beti.
-k definitutako planoan egoten da beti.
Bektore horren ibilbidea kurba lau bat izaten da beti.
a) 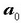 eta
eta 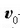 -k
norabide eta noranko bera baldin badute, orduan haien ibilbidea
-k
norabide eta noranko bera baldin badute, orduan haien ibilbidea
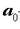 -ren
norabide eta noranzko bera duen zuzen batera murrizten da.
-ren
norabide eta noranzko bera duen zuzen batera murrizten da.
b) Hasierako lastertasuna zero baldin bada, orduan
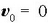 ,
eta (2.52) ekuazioa ekuazio honetara mugatzen da:
,
eta (2.52) ekuazioa ekuazio honetara mugatzen da:

Ibilbidea ere 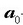 -ren
norabide eta noranzko bera duen zuzen bat da. Haren ekuazioa denboraren arabera honela adierazten da:
-ren
norabide eta noranzko bera duen zuzen bat da. Haren ekuazioa denboraren arabera honela adierazten da:

Azelerazio uniformea duen mugimendu zuzen bat da beraz.
2.13 Zenbaki lastertasun konstantea duen kurba mugimendua
Ibilbidean zehar lastertasunaren zenbaki balioak konstante irauten baldin badu, orduan
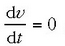 eta
eta 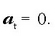 .
Puntuaren azelerazio osoa azelerazio normalera mugatzen da:
.
Puntuaren azelerazio osoa azelerazio normalera mugatzen da:

Azelerazio bektore hori elkarzuta da beraz puntuaren ibilbideari buruz, eta makurdura erradioaren alderantzizko proportzioan aldatzen da. Kurba mugimendu uniformearen ekuazioa ekuazio honetatik ateratzen da:
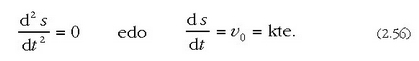
eta horren integrazioa eginez gero, hau ateratzen da:

2.14 Mugimendu zuzena
Puntuaren ibilbidea lerro zuzen bat baldin bada, orduan =
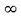 eta
eta
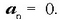 Puntuaren lastertasun erabatekoa ukitze azeleraziora murrizten da:
Puntuaren lastertasun erabatekoa ukitze azeleraziora murrizten da:
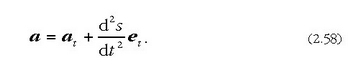
Mugimendu zuzena uniformea baldin bada gainera, azelerazio erabatekoa zero da, zeren eta
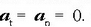 Lastertasuna orduan konstantea
da magnitudez, norabidez eta noranzkoz
Lastertasuna orduan konstantea
da magnitudez, norabidez eta noranzkoz
2.15 Zirkunferentzia baten gaineko mugimendua
Zirkunferentzia baten gaineko mugimenduak baldintza hau bete behar du beti:

alegia, azelerazio normalak lastertasun zuzenaren berreduraren proportzionala izan behar du.
2.16 Mugimendu harmoniko zuzena
x ardatzaren gainean har dezagun puntu mugikor bat, x abszisa ekuazio honek definitua daukana:

ekuazio horretan x-ek luzamendua adierazten du, puntua mugitzen ari den posizioaren
eta geldi dagoen posizioaren arteko tartea, alegia; t-k denbora, eta
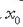
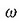
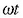 angeluak zerotik gora izan daitezkeen balio guztiak ditu (t = 0 denean), eta
angeluak zerotik gora izan daitezkeen balio guztiak ditu (t = 0 denean), eta
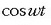 aldatu egiten da -1etik +1era bitarte. Beraz, x-ek mugitzerakoan izan dezaken gehienezko balioa
aldatu egiten da -1etik +1era bitarte. Beraz, x-ek mugitzerakoan izan dezaken gehienezko balioa
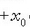 da,
eta gutxieneko balioa, berriz,
da,
eta gutxieneko balioa, berriz, 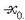 Zatiki hori lerro zuzen batean zehar mugitzen da beraz, ezkerretik eskuinera, eta eskuinetik ezkerrera, abszisatzat
Zatiki hori lerro zuzen batean zehar mugitzen da beraz, ezkerretik eskuinera, eta eskuinetik ezkerrera, abszisatzat
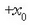 eta
eta 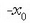 dituzten A eta B puntuen artean (2.11 irudia). O oszilazio gunetik puntu hori gehienez higitu den tartea
adierazten duen
dituzten A eta B puntuen artean (2.11 irudia). O oszilazio gunetik puntu hori gehienez higitu den tartea
adierazten duen 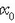 konstanteari oszilazioaren hedadura esaten zaio. Bitarte esaten zaio zatiki horrek
A-tik B-raino mugitzeko eta A puntura berriz itzultzeko behar duen denborari,
dardara oso bat egiteko behar duen denborari, alegia. T letraz adierazten da.
konstanteari oszilazioaren hedadura esaten zaio. Bitarte esaten zaio zatiki horrek
A-tik B-raino mugitzeko eta A puntura berriz itzultzeko behar duen denborari,
dardara oso bat egiteko behar duen denborari, alegia. T letraz adierazten da.
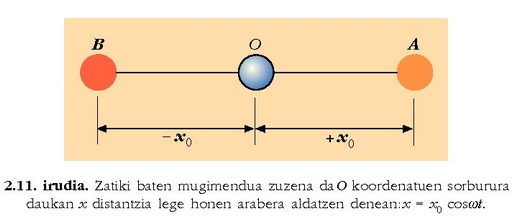
2.11. irudia. Zatiki baten mugimendua zuzena da O koordenatuen sorburura daukan x distantzia lege honen arabera aldatzen denean: x = x0 cos?t
Maiztasuna esaten zaio segundo batean egiten diren dardara osoen kopuruari. n letra grekoaz adierazten da. Bitartearen eta maiztasunaren definizioetatik ondorio hau ateratzen da:
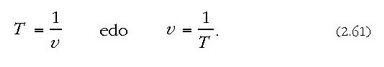
Maiztasunaren oinarrizko banakoa s 1 edo Hertz da (Hz) = oszilazioa segundoko. Oszilazio oso bati ziklo esaten zaionez, maiztasuna honela adierazten da: zikloak segundoko (cps).
Baldin t denbora 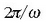 gehitzen bada, formula hau aterako da:
gehitzen bada, formula hau aterako da:
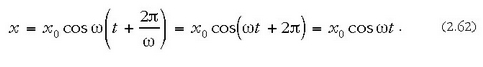
Beraz, denbora bitarte horren ondoren, x-ek lehengo balio bera du berriro. Bitarte hori mugimenduaren T bitartearen berdina da. Beraz,
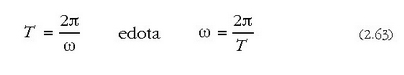
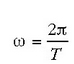 faktoreari angelu (edo zirkulu) maiztasuna esaten zaio,eta radiana segundoko 1 du neurri banakoa.
faktoreari angelu (edo zirkulu) maiztasuna esaten zaio,eta radiana segundoko 1 du neurri banakoa.
(2.61) eta (2.63) ekuazioen arabera, ondorio hau ateratzen baita

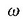 konstanteak
konstanteak 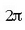 segundotan izan diren dardara kopurua adierazten du.
segundotan izan diren dardara kopurua adierazten du.
(2.60) ekuaziotik ondorio hau ateratzen da:
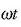 angeluak definitzen du edozein unetan puntuaren posizioa. Nolanahi ere, ekuazio horrek ez du balio,
non eta denbora neurtzen hasten ez bada puntua A puntutik igarotzen den unean.
Baina hori ez da beti gertatzen. t = 0 denean, puntu mugikorra ez baldin badago A puntuan,
orduan hau izango da puntu horren posizioa:
angeluak definitzen du edozein unetan puntuaren posizioa. Nolanahi ere, ekuazio horrek ez du balio,
non eta denbora neurtzen hasten ez bada puntua A puntutik igarotzen den unean.
Baina hori ez da beti gertatzen. t = 0 denean, puntu mugikorra ez baldin badago A puntuan,
orduan hau izango da puntu horren posizioa:

(2.65) ekuazioak, beraz, mugimendu harmoniko soil bat adierazten du, (2.60) ekuazioak baino definituagoa.
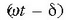 angeluari mugimenduaren fasea esaten zaio. t = 0 denean,
angeluari mugimenduaren fasea esaten zaio. t = 0 denean,
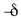 alegia,
fasearen balioari hasierako fasea esaten zaio.
alegia,
fasearen balioari hasierako fasea esaten zaio.
Oharra. Baldin eta 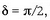 (2.65) ekuazioa
(2.65) ekuazioa 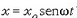 bihurtzen da;
sinu funtzioak ere dardarazko mugimendu harmonikoa definitzen du, alegia;
eta hasierako fasearen balioa du aurrekoarekiko alde bakarra.
bihurtzen da;
sinu funtzioak ere dardarazko mugimendu harmonikoa definitzen du, alegia;
eta hasierako fasearen balioa du aurrekoarekiko alde bakarra.
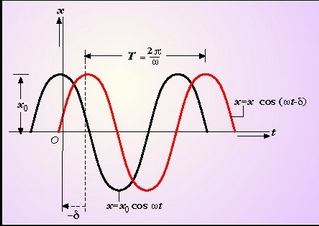
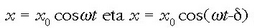 x = x0 coswt eta x = x0 cos(wt-d) ekuazioek definitzen dituzten mugimenduak
2.12 irudian irudikatu dira. Bi mugimendu horietan fase
diferentzia konstantea da eta d balio du.
x = x0 coswt eta x = x0 cos(wt-d) ekuazioek definitzen dituzten mugimenduak
2.12 irudian irudikatu dira. Bi mugimendu horietan fase
diferentzia konstantea da eta d balio du.
Batzuetan komeni izaten da 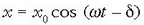 ekuazioa era honetara idaztea
ekuazioa era honetara idaztea
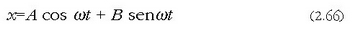
formula horretan 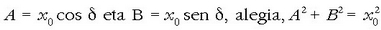
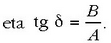
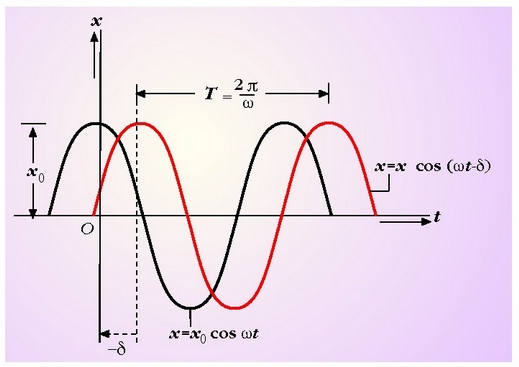
2.12. irudia. (2.60) eta (2.65) ekuazioek definitzen dituzten dardarazko mugimendu harmonikoak irudikatzen dituen grafikoa.
2.17 Lastertasuna eta azelerazioa mugimendu harmonikoan
Lege senoidal batek aldatzen ditu ez bakarrik luzamendua, baita lastertasuna eta azelerazioa ere. (2.65) ekuazioa denborari buruz deribatuz gero, lastertasunak balio hau du:
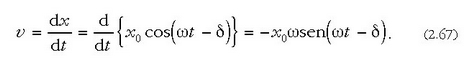
Lastertasuna deribatuz gero, azelerazioak formula hau du:
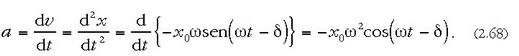
(2.65) eta (2.68) ekuazioak konparatuz gero, ekuazio hau ateratzen da:

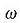 beste konstanterik ez duena. (2.69) ekuazioak hau adierazten du: azelerazioa,
une bakoitzean, x luzamenduaren proportzionala da eta kontrako noranzkoa du.
Tasun hori berezkoa du mugimendu harmonikoak.
beste konstanterik ez duena. (2.69) ekuazioak hau adierazten du: azelerazioa,
une bakoitzean, x luzamenduaren proportzionala da eta kontrako noranzkoa du.
Tasun hori berezkoa du mugimendu harmonikoak.
(2.65) eta (2.67) ekuazioak konparatuz gero,
lastertasunak 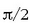 radianeko fase diferentzia du luzamenduarekiko, 90° alegia; eta (2.65) eta (2.68) konparatuz gero,
azelerazioak
radianeko fase diferentzia du luzamenduarekiko, 90° alegia; eta (2.65) eta (2.68) konparatuz gero,
azelerazioak 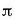 radianeko fase diferentzia du luzamenduarekiko, 180° alegia.
radianeko fase diferentzia du luzamenduarekiko, 180° alegia.
2.18 Bektore birakor baten proiekzioaz dardarazko mugimendu harmoniko bat irudikatzea
Demagun 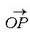 bektorea:
bektorea:
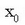 modulu konstantea du,
eta O-ren inguruan biraka dabil w angelu lastertasun konstantez (2.13 a irudia).
modulu konstantea du,
eta O-ren inguruan biraka dabil w angelu lastertasun konstantez (2.13 a irudia).
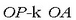 erradio finkoarekin eratzen duen
erradio finkoarekin eratzen duen
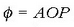 angelua handitu egiten da denboraren proportzioan.
angelua handitu egiten da denboraren proportzioan.
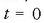 denean
denean
 da,
P puntuaren M proiekzioak abzisa hau da OA ardatzean:
da,
P puntuaren M proiekzioak abzisa hau da OA ardatzean:

M proiekzio horrek dardarazko mugimendu harmoniko soila egiten du, eta mugimendu horren anplitudea erradioaren berdina da.
Aurreko formula horrek soil-soilik balio du t =0 denean eta P puntua A-n dagoenean. Baina t =0 denean P puntua
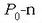 dago (2.13 b irudia), orduan
dago (2.13 b irudia), orduan 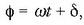 non d f-ren balioa baita t=0 denean, eta P puntuaren proiekzioak balio hau izango luke OA ardatzean:
non d f-ren balioa baita t=0 denean, eta P puntuaren proiekzioak balio hau izango luke OA ardatzean:
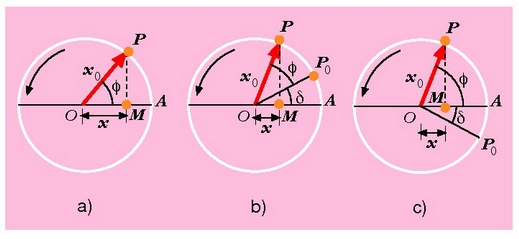
2.13. irudia. Mugimendu zirkular uniformeak sortzen duen dardarazko mugimendu harmonikoa.

t =0 denean, P puntua 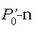 egongo balitz
egongo balitz 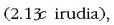 , orduan
, orduan
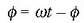 eta
eta

2.19 Inertzia sistemak
Gauza jakina da gorpuzki puntu baten mugimendua deskribatzeko erreferentzia sistema bat dagoela aukeratu beharra, hari esker jakingo baita puntu horrek espazioan duen posizioa. Baina nola sistema bakoitzean lege naturalak formaz desberdin izaten diren oro har, gerta daiteke, baldin eta erreferentzia sistema arbitrario bat aukeratzen bada, lege horiek, diren eta soilenak izanik ere, forma konplexuak izatea. Horregatik lege naturalek formarik soilena izango duten erreferentzia sistemak bilatu behar dira.
Badira erreferentzia sistema azeleratu gabeak, bata besteari buruz magnitudez, norabidez eta noranzkoz lastertasun konstantez mugitzen direnak, alegia. Inertzia sistemak esaten zaie horiei. Gure eguzki sisteman, eta esperientziaren arabera, inertzia sistemak Eguzkiaren erdigunea du sorburu eta finkotzat hartzen diren hiru izarretara orientatutako erdi zuzenak ditu ardatz. Inertzia sistema horri lehen mailako inertzia sistema esaten zaio.
Errotaziorik gabe, eta lehen mailako inertzia sistemari buruz lastertasun konstantean mugitzen den beste edozein sistemari bigarren mailako inertzia sistema esaten zaio. Problema praktiko gehienetan, Lurrari zorrotz lotutako erreferentzia sistema bat aukera daiteke bigarren mailako inertzia sistematzat. Erreferentzia sistema hori ez da berez inertzia sistema, zeren eta Lurrak, bere ardatzaren inguruan biraka dabilen bitartean, orbita bat egiten baitu Eguzkiaren inguruan.
Bigarren mailako inertzia sistema baten eta lehen mailako inertzia sistema baten artean dagoen harremana zein
den jakiteko, Oxyz ardatz finkoko sistema bat marraztu behar da lehen mailako inertzia sisteman,
eta Oxyz ardatz finkoko sistema bat bigarren mailako inertzia sisteman.
Demagun, gainera, bigarren mailako inertzia sistema lehen mailako inertzia sistemari buruz V lastertasun
konstantez mugitzen dela. r izanik A zatiki baten posizio bektorea Oxyz sistemari buruz, eta r'
zatiki horren beraren posizio bera O'x'y'z' sistemari buruz (2.14 irudia), baldin eta
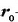 -k O'-ren
posizio bektorea adierazten badu O-ri buruz, orduan:
-k O'-ren
posizio bektorea adierazten badu O-ri buruz, orduan:

Baina O' lastertasun konstantez mugitzen denez, orduan:
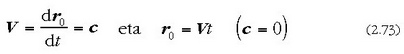
non, errazago ari ahal izateko, uste izan baitugu t =0 denean O-ren eta O-ren sorburuak bat egiten dutela, eta, beraz, c integrazioaren konstantearen balioa zero dela.
(2.72) eta (2.73) ekuazioetetik hau ateratzen da:

edo bestela,
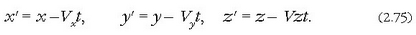
Bi koordenatu sistemak erlazionatzen dituzten aurreko ekuazio horiei transformazio ekuazio klasikoak edo Galileoren transformazioak esaten zaie.
A puntuaren lastertasuna zein den jakiteko, (2.74) ekuazioa deribatu behar da denborari buruz. Hau da emaitza:

ekuazio horretan v-k A zatikiak lehen mailako inertzia sitemari buruz duen lastertasuna adierazten du, eta v-k zatiki horrek berak bigarren mailako inertzia sistemari buruz duena. V=ete denez, (2.76) ekuazioa berriz deribatuz gero hau ateratzen da:

alegia, A zatikiak azelerazio bera du bi erreferentzia sistema horietan, edo, bestela esanda, azelerazioak ez du aldaketarik erreferentzia sistema batetik lehenengoari buruz errotaziorik gabe eta lastertasun konstantez mugitzen den beste erreferentzia sistema batera igaroz gero.
Arestian atera dugun ondorioan esperientziaren araberako hipotesi batzuk eman ditugu. Lehenik, (2.72) deribatu dugunean, ontzat eman dugu bi ikuslek gauza bera ikusten dutela, bata bestearekiko mugimendu erlatiboarekin, bi punturen arteko distantzia neurtzen dutenean, une jakin batean, (erabiltzen dituzten erregelak ez dira mugimendua bitartean ez luzatzen ez laburtzen). Bigarrenik, ontzat eman dugu orobat denbora eskala berbera dutela bi erreferentzia sistema horiek. Azken hipotesi hori (2.75) ekuazioei laugarren ekuazio bat erantsiz adieraz daiteke:

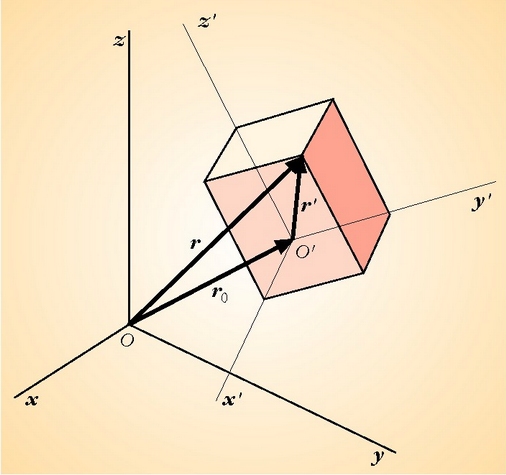
2.14. irudia. A zatiki batek azelerazio bera du Oxyz lehen mailako inertzia sisteman eta Oxyz bigarren mailako inertzia sisteman
DARDARAZKO MUGIMENDUEN OSAERA
2.20 Sarrera
Sistema jakin batzuetan zatiki batek dardarazko bi mugimendu independente egin ditzake aldi berean.
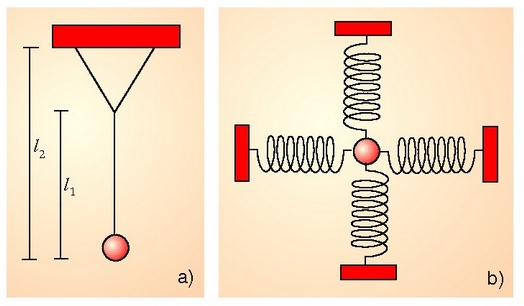
2.15. irudia. a) Aldi berean bi pendulu mugimendu elkarzut egiten dituen masa puntua. b) Aldi berean dardarazko bi mugimendu elkarzut egiten dituen masa puntua.
2.15 a) irudian puntu masa batek l1 luzerako pendulu soil baten gisa oszilatzen du irudi horretako planoan, eta l2 luzerako pendulu soil baten gisa oszilatzen du plano horri buruz zut dagoenean.
2.15 b) irudian puntu masak dardarazko bi mugimendu elkarzut egiten ditu aldi berean.
Orain dardarazko mugimenduen osaerak dauzkan kasu garrantzitsuenak adieraziko dira.
2.21 Norabide bereko dardarazko bi mugimenduen osaera
Puntu batek dardarazko bi mugimendu harmoniko egiten dituenean aldi berean, horrela sortzen den mugimendua gainjartzearen printzipioa aplikatuz definitzen da. Printzipio horren arabera, puntuak une jakin batean egiten duen lekualdatzea, bi mugimendu horiek zeinek bere aldetik egingo luketen lekualdatzearen batura da. Oro har, dardarazko bi mugimendu horiek anplitude, maiztasun eta fase desberdinak dituzte.
a) Bi dardarek maiztasun eta fase berdinak dituzte, baina anplitude desberdinak. Ekuazio hauetatik
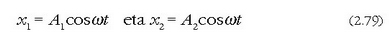
ekuazio hauek ateratzen dira:
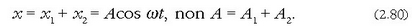
Horren ondorioz ateratzen den dardarazko mugimenduaren A anplitudea eta mugimendu osagaien anplitudeen batura berdinak dira (2.16 irudia).
b) Bi dardara horiek maiztasun eta anplitude berberak dituzte, baina fase diferentzia dago haien artean. Beraz, ekuazio hauetatik
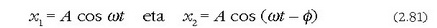
beste hauek ateratzen dira:
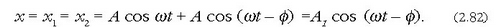
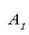 eta f definitzeko, (2.82) formulan agertzen diren kosinuak garatu behar dira, eta terminoak
eta f definitzeko, (2.82) formulan agertzen diren kosinuak garatu behar dira, eta terminoak 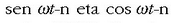 biltzen dira. t-k izan ditzakeen balio guztietarako (2.82) ekuazioa bete egiten da, baldin eta
biltzen dira. t-k izan ditzakeen balio guztietarako (2.82) ekuazioa bete egiten da, baldin eta
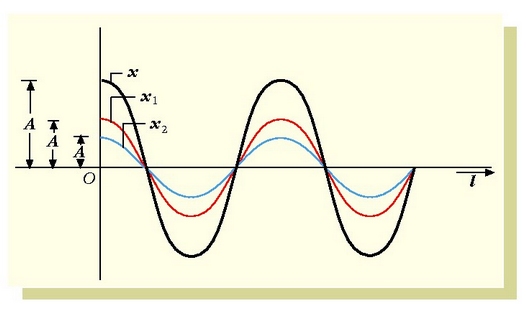
2.16. irudia. Maiztasun eta fase bereko baina anplitude desberdineko bi dardaren osaera.

Aurreko ekuazioak ebatzita emaitza hauek ateratzen dira:
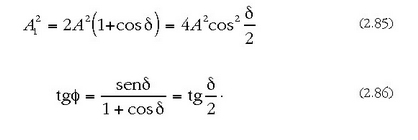
Beraz:
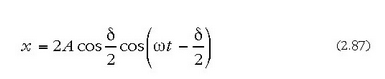
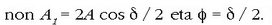 Beraz, hor ateratzen den dardara ere harmonikoa da, eta haren anplitudea,
Beraz, hor ateratzen den dardara ere harmonikoa da, eta haren anplitudea,
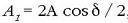 ,
osagai dituen dardaren anplitudeen batura baino txikiagoa da.
,
osagai dituen dardaren anplitudeen batura baino txikiagoa da.
Batez ere, baldin eta 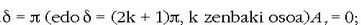 ;
alegia, fase oposizioan dauden bi dardara konpentsatu egiten dira, eta puntu hori geldirik dago (2.17 a irudia).
Baldin eta
;
alegia, fase oposizioan dauden bi dardara konpentsatu egiten dira, eta puntu hori geldirik dago (2.17 a irudia).
Baldin eta 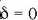 ,
bi dardara horiek fasean daudela esaten da, eta anplitudea orduan gehienezkoa izango da,
,
bi dardara horiek fasean daudela esaten da, eta anplitudea orduan gehienezkoa izango da,
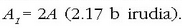 Tarteko kasuetan, anplitudeak 0tik 2A bitarteko balioa du. Fase diferentzia
Tarteko kasuetan, anplitudeak 0tik 2A bitarteko balioa du. Fase diferentzia
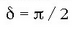 denean,
bi dardara horiek koadraturan daude (2.17 c irudia).
Bereziki,
denean,
bi dardara horiek koadraturan daude (2.17 c irudia).
Bereziki, 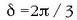 denean,
ondorioz sortzen den dardararen anplitudeak A balio du (2.17 d irudia).
denean,
ondorioz sortzen den dardararen anplitudeak A balio du (2.17 d irudia).
c) Bi dardara horiek anplitude berak dituzte, haien hasierako faseek zero balio dute (soil adierazteko) eta haien maiztasunak desberdinak dira. Orduan, ekuazio honetatik
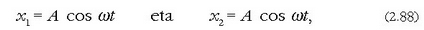
ekuazio hau ateratzen da:
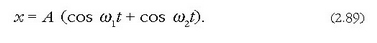
Baldin eta formula hauen bidez
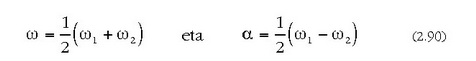
batez besteko zirkulu maiztasun bat definitzen bada,
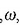 eta modulaziozko angelu maiztasun bat,
eta modulaziozko angelu maiztasun bat,
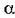 , ekuazio honetatik
, ekuazio honetatik
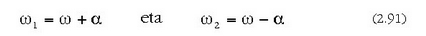
ekuazio hau ateratzen da:
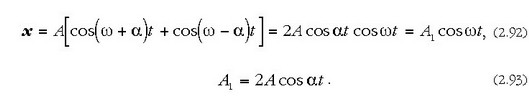
jarri baitugu bertan.
Baldin eta 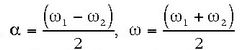 baino txikiagoa baldin 2 2 bada, orduan (2.92) ekuazioak adierazten duen mugimendua w maiztasun
zirkularra berdin osagai dituen dardaren baturaren erdia duen dardaratzat har daiteke;
dardara horren anplitudea, formula, aldatu egiten da denbora pasa ahala, osagai dituen
dardarenarteko aldearen erdia balio duen maiztasun zirkularraz. Ondorioz
sortzen den dardararen maiztasunak hau balio du:
baino txikiagoa baldin 2 2 bada, orduan (2.92) ekuazioak adierazten duen mugimendua w maiztasun
zirkularra berdin osagai dituen dardaren baturaren erdia duen dardaratzat har daiteke;
dardara horren anplitudea, formula, aldatu egiten da denbora pasa ahala, osagai dituen
dardarenarteko aldearen erdia balio duen maiztasun zirkularraz. Ondorioz
sortzen den dardararen maiztasunak hau balio du:
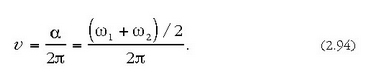
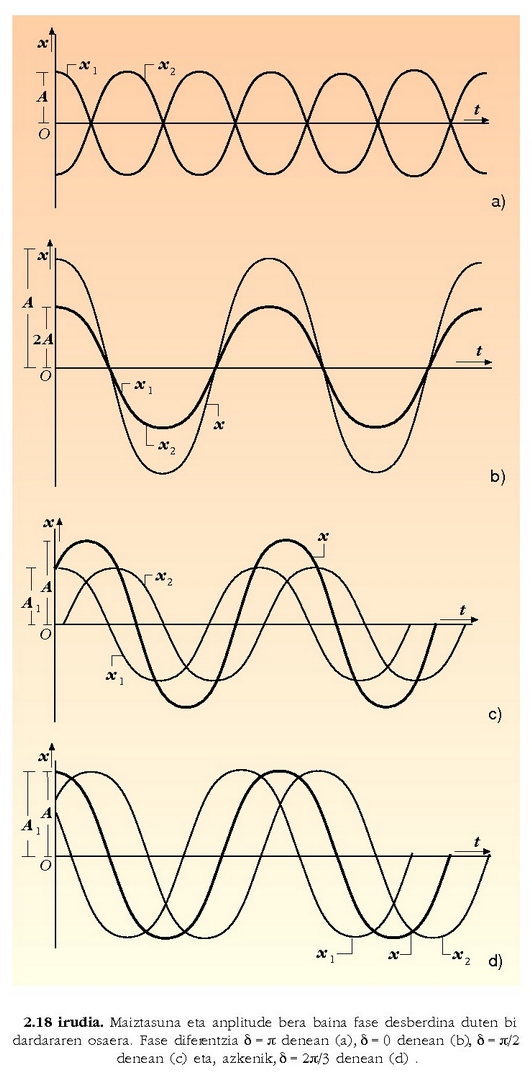
eta 0tik 2A-ra bitartera aldatzen da. Dardara mota horri pultsazio esaten zaio, eta 2.18 irudian dago irudikatua.
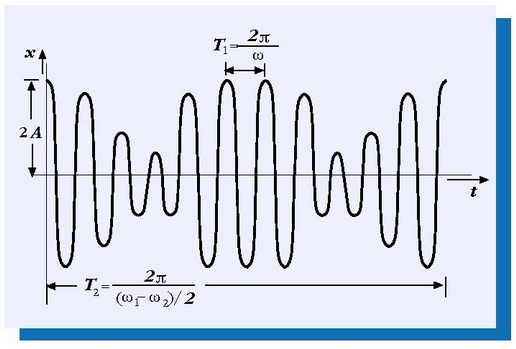
2.18. irudia. Anplitude bera, hasierako fasea zero baliokoa, eta maiztasunak elkarren zertxobait desberdinak dituzten bi dardara mugimenduk pultsazio izeneko dardara bat sortzen dute
2.22 Bi dardara mugimendu lauki zuzenen osaera
Bada dardara mugimendu garrantzitsu bat, bi dardara mugimendu lauki zuzenen aldi bereko eragina duen puntu batek egiten duena. Demagun
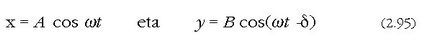
direla mugimendu horietako bakoitza adierazten duten ekuazioak. Ekuazio horietatik t parametroa kenduz gero, ibilbidearen ekuazioa ateratzen da koordenatu kartesiarretan. Horietako lehenengo ekuaziotik hau ateratzen da:

eta bigarrenean ordezkatuz, hau ateratzen da:
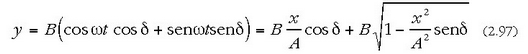
edo bestela,
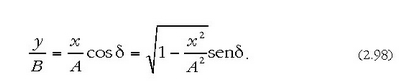
Aurreko ekuazio hori berretuz, hau ateratzen da:
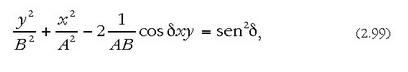
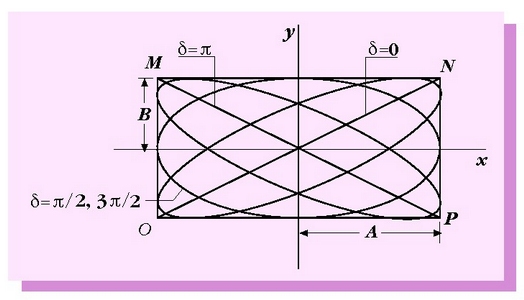
2.19. irudia. Bi dardara lauki zuzenen osaera. Ibilbidea fase diferentziaren araberakoa da
Ekuazio horrek, oro har, haren ardatz nagusiek koordenatu ardatzekin bat egiten ez duten elipse bat adierazten du. (2.95) ekuazioaren arabera, x-ek -A eta +A mugen tartean egon behar duenez, eta y-k, berriz, -B eta +B-ren mugen artean, elipsea beti dago alde hauek dituen lauki zuzenaren baitan:
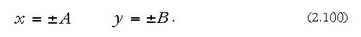
Ibilbidearen forma d-ren balioaren araberakoa da (2.19 irudia).
a) 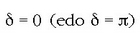 baldin bada, orduan
baldin bada, orduan 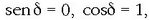 ,
eta dardara eliptikoa dardara zuzen bihurtzen da, (2.95) ekuazioa ekuazio honetara murrizten baita:
,
eta dardara eliptikoa dardara zuzen bihurtzen da, (2.95) ekuazioa ekuazio honetara murrizten baita:

ekuazio horrek lerro zuzen bat adierazten du; lerro hori sorburutik igarotzen da eta bere maldak B/A balio du
( 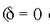 denean,
MP lerro zuzena ateratzen da, eta d denean, NQ lerro zuzena).
denean,
MP lerro zuzena ateratzen da, eta d denean, NQ lerro zuzena).
b) Baldin eta 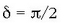 bada, alegia, y dardara fasea t =0 unean bitarte laurden bat baldin bada, orduan
bada, alegia, y dardara fasea t =0 unean bitarte laurden bat baldin bada, orduan
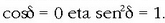 Elipsearen ekuazioak era honetara adierazten da orduan:
Elipsearen ekuazioak era honetara adierazten da orduan:

alegia, elipse horrek ardatz koordenatuak ditu ardatz nagusitzat. Ardatz nagusiak, beraz, norabide horietan osagai diren dardaren anplitudeen berdinak dira. Batez ere, baldin eta A = B, ekuazio hori ekuazio hau bihurtzen da:

eta ibilbidea, kasu horretan, erdigunea koordenatuen sorburuan duen zirkunferentzia bat da.
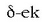 aurreko baldintza bat bera betetzen ez duenean, hor sortzen den mugimendua eliptikoa izango da,
eta koordenatuen erdigunea elipsearen erdigunea izango da.
aurreko baldintza bat bera betetzen ez duenean, hor sortzen den mugimendua eliptikoa izango da,
eta koordenatuen erdigunea elipsearen erdigunea izango da.
Elipsea zer noranzkotan dagoen jakiteko, (2.95) ekuazioak erabiltzen dira.
t =0 denean, orduan, t gehitzean x gutxitu egiten da, baina y gehitu egiten da y
ardatzaren norabide positiboan 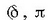 baino txikiago baldin bada). Dardara forma horri dardara eliptiko lebogiroa esaten zaio.
Baldin eta
baino txikiago baldin bada). Dardara forma horri dardara eliptiko lebogiroa esaten zaio.
Baldin eta 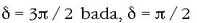 denean sortzen den elipse bera sortzen da hemen ere, baina orduan kurba alderantzizko noranzkoan dago,
eta dardara horri dardara eliptiko destrogiroa esaten zaio.
denean sortzen den elipse bera sortzen da hemen ere, baina orduan kurba alderantzizko noranzkoan dago,
eta dardara horri dardara eliptiko destrogiroa esaten zaio.
Eratzen diren dardara elkarzutek maiztasun desberdina dutenean,
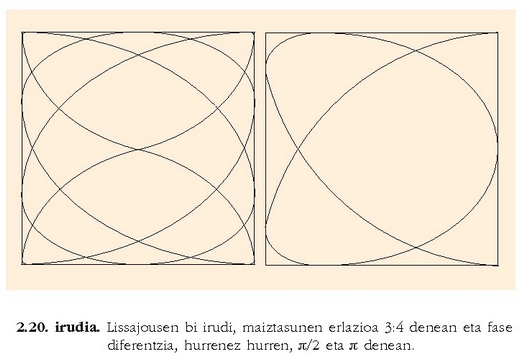
oso kurba desberdinak sortzen dira, eta Lissajousen irudiak esaten zaie.
2.20 irudian Lissajousen bi irudi marraztu dira, maiztasunen erlazioa 3:4 denean eta fase diferentzia,
hurrenez hurren, 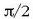 eta
eta 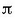 denean.
denean.



