Matematika»Aritmetika

3. Atala

Irudikariak baliapide dotore zoragarria diragiza adimenarentzat, "contra natura "zko jaiotza batpentsamenduaren alorrean, izatearen eta ez izatearen artekoanfibio bat ia-ia. (Leibniz 1646-1716).

I. Zenbaki konplexuak. Sarrera

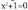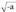Gauza jakina denez, bigarren mailako ekuazio batzuek ez dute soluzio errealik izaten,ekuazioak adibidez. Ekuazio honek soluziorik balu,izango litzateke soluzio hori.Jeronimo Cardanok (1501-1576), hirugarren mailako ekuazioak ebatzi ahal izateko, bigarren mailako edozein motatako ekuazioak ebatzi behar izaten zituen. Horrela,erabiltzen zuen kalkuluak egiterakoan, ez ordea ebazpenak azaltzerak oan.1572. urtean, Bombelikzela ikusi zuen.Horri esker, geroago, zenbaki negatiboen erro karratuak, "zenbaki irudikariak", onartu ziren. Ia mende oso bat pasa zen zenbaki konplexuen ikasketa sakona egin arte. Ikasketa honen ondorio bezala, gaur egun zenbaki konplexuen gorputza deritzanera iritsi ziren.Zenbaki konplexuei buruz dagoen teoremarik garrantzitsuena, "Algebraren oinarrizko teorema", Carl Friederich Gaussek (1777- 1855) frogatu zuen. Teorema honek, koefiziente konplexuak dituen edozein polinomiok, erro edo soluzio bat duela dio.Unitate irudikari bere berbidura -1, hau dabetetzen duen i izate abstraktuari deitzen zaio.Elementu hau zenbaki errealen gorputzari gehituz gero,ekuazioak soluzio bat baduela ikusten da, baina zenbaki errealen arteko batura eta i eta zenbaki errealen arteko biderkadura kalkulatzeko prozedurarik gabe gelditzen gara.Biderkaketak egin ahal izateko b zenbaki erreala eta i unitate irudikaria emanik, bi biderkadurak existitu beharko du.Bestalde, azken zenbaki hauek zenbaki errealekin batu ahal izateko, a zenbaki erreala emanik, a+bi elementuak existitu beharko du.Horrela, a+bi erako edozein adierazpeni zenbaki konplexu deitzen zaio, a eta b zenbaki errealak direlarik.

Adibidez,zenbaki konplexuak dira.Hona iritsi ondoren, problema hau jar daiteke : "Bi adierazpen desberdinek emaitza bera eman al dezakete?. Ezezko erantzuna duela ikusiko da.a + bi = c + di bada, a - c = (d - b) i izango da. Bi atalak ber bi eginez: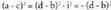aterako da. Lehenengo atala (berbidura bat denez), 0 edo handiagoa izango da ; eta bigarren atala (ikurra aldatuta daukan berbidura bat denez), 0 edo txikiagoa izango da. Beraz, biak berdinak izan behar dutenez, biak nuluak izango dira. Hau da :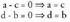

Zenbaki konplexuen berdintasuna

a + bi eta c + di bi zenbaki konplexu berdinak dira, a = c eta b = d denean.

Zenbaki konplexu baten zati erreala eta zati irudikaria

z = a + bi zenbaki konplexua emanda, a zenbakiari z-ren zati erreala, eta b zenbakiari z-ren zati irudikaria esaten zaie.Zenbaki konplexu baten zatietariko bat (erreala edo irudikaria) zero bada, zati hori ez da idazten. Horrela a + Oi zenbakiaren ordez a eta 0 + bi zenbakiaren ordez bi idatziko da.Zenbaki errealak, zati irudikaria 0 duten zenbaki konplexuak bezala har daitezke. Zati erreala 0 duten zenbaki konplexuei irudikari puru edo zenbaki irudikari esaten zaie.

I I . Zenbaki konplexuen arteko eragiketak

Zenbaki konplexuen arteko batuketa eta biderkaketa

a + bi eta c + di bi zenbaki konplexu emanda, beraien arteko batuketa eta biderkaketa honela definitzen dira :Biderkaketa, i zenbaki erreal bat balitz bezala hartuz, etadela gogoan izanik egin daiteke :

Zenbaki konplexuen arteko batuketaren tasunak

Bi zenbaki konplexuen arteko batuketak tasun hauek betetzen ditu :? Trukakorraa + bi eta c + di zenbaki konplexuak emanda, hau betetzen da :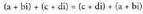? Adibidea :Beraz, berdinak dira.? Elkarkorraa + bi, c + di, eta e + fi hiru zenbaki konplexu emanda, hau betetzen da:? Adibidea :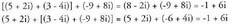Berdinak? Elementu neutroaElementu neutroa 0 + 0i zenbakia da, izan ere0 + Oi zenbakiaren ordez 0 idazten da, eta "zero" esaten zaio.? Elementu simetrikoaa + bi zenbaki konplexu baten simetrikoa (-a - bi) zenbakia da, izan ere

Zenbaki konplexuen arteko biderkaketaren tasunak

? Trukakorraa + bi eta c + di zenbaki konplexuak emanda, hau betetzen da :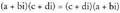? Adibidea :? Elkarkorraa + bi, c+ di, eta e + fi hiru zenbaki konplexu emanda, hau betetzen da :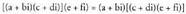? Adibidea: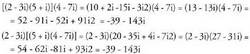? Elementu neutroaBiderkaketaren elementu neutroa 1 + 0. i zenbakia da, izan ere a r bi zenbaki konplexua emanda, hau betetzen da :Elementu neutroa bata da.? Batuketarekiko biderkaketaren banakortasun legeaa + bi, c + di, eta e + fi hiru zenbaki konplexu emanda, hau betezen da :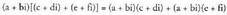? Adibidea :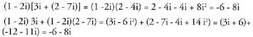Zenbaki konplexuen multzoak batuketarekiko eta biderkaketare- :iko azaldu diren tasun guztiak direla eta, eraztun trukakorraren gitura duela esaten da.Zenbaki konplexuen multzoa adierazteko C edoerabilzen? Biderkaketarekiko elementu simetrikoa0 + Oi ez den a + bi zenbaki konplexu bat emanda, badago beste enbaki konplexu bat beren arteko biderkadura biderkaketaren elenentu neutroa (1 + Oi) denaFrogapena :a + bi zenbaki konplexuaren alderantzizkoa den x + yi zenbakia .alkulatuko da.a-rekin biderkatuz :ateratzen da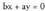b-rekin biderkatuz:ateratzen da.

Batuketa eginez: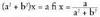Bigarren ekuazioan y bakanduz edo despejatuz: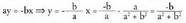z = a + bi zenbaki konplexuaren alderantzizkoaedoerabiltzen da.Beraz z = a + bi bada

Zenbaki konplexuen arteko zatiketa

Zatiketa, biderkaketaren alderantzizko eragiketa da. Hau da, bi zenbaki konplexuen arteko zatidura, lehenengoaren, eta bigarrenaren alderantzizkoaren arteko biderkaduraren berdina da.Ebatzitako ariketa (Zenbaki konplexuen arteko zatiketaren aplikazioa)Ebazpena:

I I I. Adierazpen grafikoa. konplexu konjokatua

Zenbaki konplexu baten adierazpen grafikoa

Edozein zenbaki konplexu bi zenbaki errealen bidez, bere zati erreala eta bere zati irudikariaren bidez, era bakar batean adierazi daitekeenez, a + bi edozein zenbaki konplexu (a,b) planoko puntuarekin, eta planoko (a,b) puntua a + bi zenbaki konplexuarekin pareka daiteke.Gainera, planoko (a,b) edozein puntuk, jatorria (0,0) puntuan eta muturra (a,b) puntuan duen bektorea definitzen du.Hau dela eta, edozein zenbaki konplexu planoko bektore bat bezala defini daiteke, bektore horren jatorria (0,0) koordenatu jatorria eta bere muturra zenbaki konplexuari elkartutako (a,b) bikote ordenatua delarik.

Zenbaki konplexu baten konjokatua

Zenbaki konplexu baten konjokatua, abzisa ardatzarekiko simetriaz lortutako konplexuari esaten zaio.a + bi zenbaki konplexua irudikatuz, eta dagokion simetria eginez, a - bi konjokatua lortzen da.Zenbaki konplexu bat eman da, bere konjokatua, gainean marra bat jarriz adieraz daiteke. Honela idatziko da :

Konjokatuaren tasunak

Lehenengo tasuna z zenbaki konplexu baten konjokatuaren konjokatua, z bera da.

Frogapena :? Bigarren tasuna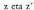bi zenbaki konplexu emanda, horien arteko baturaren konjokatua eta horien konjokatuen arteko batura berdinak dira.

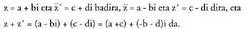Honela adierazten da hori :Frogapena :Bestalde :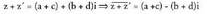Bi adierazpenak bat datoz.? Hirugarren tasunaBi zenbaki konplexuren arteko biderkaduraren konjokatua, eta zenbaki konplexu horien konjokatuen arteko biderkadura berdinak dira: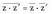Frogapena :eta honen konjokatua hau da :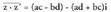Bestalde konjokatuen biderkadura kalkulatuz, hau lortzen da :Bi emaitzak berdinak dira.? Laugarren tasunaBere konjokatuarekin bat datozen konplexuak zenbaki errealak dira.Frogapena :Izan bedi a + bi, bere konjokatuarekin bat datorren zenbaki konplexua.

Orduana + bi = a - bi izango da.Baina hau b = 0 denean bakarrik beteko da ; hau da, a + bi zenbaki erreala denean.? Bosgarren tasunaZenbaki konplexu baten eta bere konjokatuaren arteko batura eta biderkadura, biak zenbaki errealak dira.Frogapena :

Zenbaki konplexuen arteko zatiketa

Azken tasun honetaz baliatuz, zatidura, zenbakitzailea eta izendatzailea, izendatzailearen konjokatuarekin biderkatuz kalkula daiteke.

Adibidez,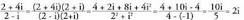Ebatzitako ariketa (Zenbaki konplexuen arteko zatiketaren aplikazioa)Bilatu k-ren balioa,zatidura :a) Erreala izan dadin.b) Irudikari purua izan dadin.

Ebazpenaa) Zati irudikaria 0 denean, zatidura zenbaki erreala izango da, beraz:b) Zati erreala zero denean, zatidura zenbaki irudikari purua izango da, beraz :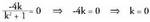

I V - Zenbaki konplexu baten era trigonometrikoa eta era polarra

Lehentxeago azaldu den bezala, zenbaki konplexu bat bektore bezala adieraz daiteke. Hau dela eta, bektorea, bere moduluaren eta bektoreak abzisa-ardatzaren alde positiboarekin eratzen duen a angeluaren bidez era bakar batean definitzen da.z = a + bi era binomikoan emandako zenbaki konplexu bat izanik, eta Iz1 bere moduluari, eta a bere argumentu edo eratzen duen angeluari deituz, erlazio hauek lortzen dira :Berdintasun hauetan a eta b bakanduz edo despejatuz,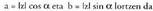Hau dela eta :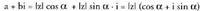Edozein z zenbaki konplexu,erako adierazpen baten bidez adieraz daiteke. Zenbaki konplexu bat idazteko era honi era trigonometrikoa deitzen zaio.Kasu askotan modulua eta argumentua bakarrik idazten dira, azkena, azpiindize bezala jartzen delarik. Horrela

Zenbaki konplexu baten modulua eta argumentua kalkulatzeko era

z = a + bi zenbaki konplexuaren argumentua kalkulatzeko, kontuan hartu behar dadela, etadela.Bi berdintasun hauen arteko zatiketa eginez :Horrela, konplexu baten argumentua bere tangenteak F(b ;a) balio duen angelua bat da.Oro har, 0° eta 360° angeluen artean, tangentearen balio bera duten bi angelu izango dira. Zein aukeratu behar den zehazteko, emandako zenbaki konplexua dagoen koadrantea zein den zehaztu behar da.Modulua kalkulatzeko, lortutako berdintasunetako berbidura edo karratuak batzen dira :Ebatzitako ariketak (Zenbaki konplexu bat idazteko era desberdinak)1. Idatzi era polarrean zenbaki konplexu hauek :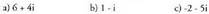Ebazpena :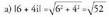Kalkulagailua erabiliz,Balio bera-ko aldea duten bi angeluk betetzen dutela kontuan izanik,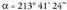ere onar zitekeen.Baina eman diguten zenbaki konplexua lehenengo koadrantean dago.Beraz,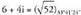duten angeluak 135° eta 315° dira. Emandako zenbaki konplexua laugarren koadrantekoa denez, argumentua 315° da.

Berazduten bi angeluak 68° 11' 54" eta 248° 11' 54" dira. Baina emandako zenbaki konplexua hirugarren koadrantekoa denez,' argumentu bezala bigarren balioa hartu behar da.

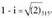
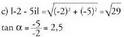
Beraz,Ebazpena: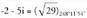

Zenbaki konplexuen arteko biderkaketa era polarrean

Zenbaki konplexuen arteko biderkaketa kalkulatzeko metodo bat ikusi bada ere, bi zenbaki konplexu era modulu-argumental edo polarrean emanda daudenean, biderkadura kalkulatzeko metodo errazago bat erabil daiteke. Metodo hau erabiltzen denean, zenbaki konplexuen moduluak biderkatu eta argumentuak batu egiten dira.Egindakoa zuzena dela ikusteko, biderkaketa egitea nahikoa da :Baina parentesi artean azaldutakoakangeluaren arrazoi trigonometrikoak dira. Honela bada :Ebatzitako ariketak1. Bi zenbaki konplexuren arteko zatiketa egiteko, beren moduluen zatiketa eta beren argumentuen kenketa egin behar dela frogatu.Ebazpena : Eman dezagunetazenbaki konplexuak zatitu nahi ditugula. Zatiduraren moduluari (z" ( eta bere argumentuari (" deitzen badiegu :Beraz:2. Kalkulatu 2i eta 2 + 2i zenbaki konplexuen arteko biderkaketa, ikusitako bi erak erabiliz.Ebazpena :? Lehenengo eran, bi zenbakiak zuzen zuzenean biderkatzen dira :? Bigarren era burutzeko, aurretik, bi zenbaki konplexuak era polarrean jarri behar dira :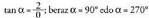izan daiteke, baina ordenatua positiboa denez,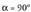izango da,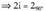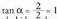beraz,edoizan daiteke, baina zenbaki konplexua lehenengo koadrantekoa denez,izango daEra polarrean biderkaketa eginez :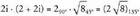Azken emaitza hau era polarretik era binomikora pasatzen bada,3. Zenbaki konplexu baten eta bere konjokatuaren arteko biderkadura moduluaren berbia edo karratua dela frogatu.Ebazpena :Bi frogapen egingo dira :b) Zenbaki konplexua era polarrean ematen badigute, bere modulua IRI eta argumentua a izango da. Aldameneko irudian ongi ikusten denez, emandako zenbaki konplexuaren konjokatuak modulu bera izango du Izl, baina bere argumentua 360°da.Biderkaketa eginez :

V. Zenbaki konplexu baten berreketa eta erroketa. Moivreren formula

Zenbaki konplexu baten n. berredura beste zenbaki konplexu batda, non modulu berria emandako zenbaki konplexuaren moduluan. berredurara jasoaz ateratzen baita, eta argumentu berria emandakobaita. Hau da,Frogapena:Berdintza hau Moivreren formula izenz ezagutzen da, frantziar jatorrikoEbatzitako ariketa (Moivreren formularen aplikazioa)Moivreren formula erabiliz, kalkulatu sin 4x eta cos 4x, x-enarrazoi trigonometrikoen arabera.Ebazpidea :1 x zenbaki konplexua kontuan hartuz, bere laugarren berredurakalkulatuz :BainaAzken adierazpen hau Newtonen binomioa erabiliz ateratzenbadaBaina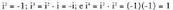Horrela :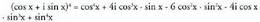Zenbaki honen zati erreala,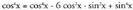da, eta zati irudikaria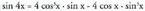

Zenbaki konplexu baten erroketa

Zenbaki konplexu baten errodurak kalkulatzeko Moivreren formulaizango direla moduluak berdinak eta argumentuen arteko aldea edodiferentzia 360°-ren anizkoitz edo multiploa denean.

Izan biteetabi zenbaki konplexu, nonBeraz,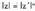izango daeta, k edozein zenbaki osoizan daitekeelarik. Orduan nBat batean badirudi infinitu soluzio aterako direla, baina k-ri n-renmultiploa den kopuru bat gehitzen bazaio, argumentu berria n-rekinzatitzerakoan, zenbait zirkunferentzia gehiago dituen argumentu ezagun bat aterako da. Beraz k-ri 1,2,3,... , balioak ematea aski da,horrela n- 1 erro edo soluzio lortzen delarik, eta k = O-ri dagokionarekinEbatzitako ariketak (Zenbaki konplexu baten errodurak)1. Bila 27 zenbaki konplexuaren erro kubikoa.Ebazpidea : Azaldutako metodoa erabili ahal izateko, zenbaki konplexua era polarrean jarri behar da. Beraz, hasteko, 27 zenbaki komplexua era polarrean jarri behar da., beraz a = 0 º edo a = 180 º izan daiteke, baina 27-ren zati erreala positiboa denez, a = 0 º izango da.

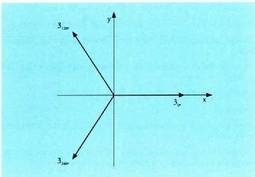
Behar diren balioak kalkulatuz: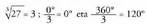Horrela, erro kubikoak, edo soluzioak, modulutzat 3 eta argumentutzat 0° + 120-k dutenak izango dira, k = 0, k = 1 edo k = 2 izan daitekeelarik.Orduan, 3 erro edo soluzioak hauek dira :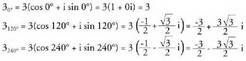2. Bila 1 + i zenbaki konplexuaren laugarren mailako errodurak.Ebazpidea :Hasteko 1 + i zenbaki konplexuaren modulua eta argumentua kalkulatzen dira :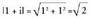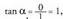. beraz eta lehenengo koadratekoa denez,izango da.Laugarren mailako erro guztien modulua :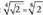izango da.Argumentua kalkulatzeko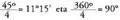kalkulatu behar da.k-ri 0, 1, 2 eta 3 balioak emanez, 1 + i zenbaki konplexuaren laugarren mailako errodurak lortzen dira.

Zenbaki konplexu baten erro karratuak

Zenbaki konplexu baten edozein mailatako erroak kalkulatzeko ikusi dugun eraz gain, era binomikoan emandako zenbaki konplexuen erro karratuak kalkulatzeko beste prozedura bat ere erabili dezakegu.

SolizioakProzedura beti berdina denez, behin azaltzea nahikoa izango da.-5 + 12i zenbaki konplexuaren erro karratuari dagozkion soluzioak kalkulatuko dira.Izan bedi a + bi soluzio horietariko bat. Orduan :Bi zenbaki konplexu horiek berdinak izango dira, zati errealak berdinak eta zati irudikariak berdinak direnean. 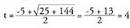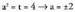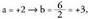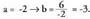Beraz :Lehenengo ekuazioan ordezkatuz,eta ekuazio hau bikarratua da.aldaketa eginez,ekuazioa lortzen da.Ekuazio honek bi soluzio ditu, bata positiboa eta bestea negatiboa, t zenbaki erreal baten berbidura denez, positiboak bakarrik dauka garrantzia.Orduan,Beraz bi soluzio ditugu :etaHori dela eta, -5 + 12i zenbaki konplexuaren erro karratuak bi soluzio hauek ditu: 2 + 3i eta -2 -3i.