Fisika-Kimika»Fisika - Kimika
DINAMIKA.2
6.Uhin Mugimendua
Uhin lauaren ekuazioa
Dimentsio bakarreko uhin batean, u(x, t) perturbazioa bi aldagairen mende dago, x kokagunearen eta t denboraren mende hain zuzen. Perturbazioa puntu finko batean bakarrik aztertu nahi denean t aldatzen da, eta x kokagunea ez da aldatzen. Aldiz, perturbazioaren azterketa une jakin bati buruz bakarrik egin nahi bada, t denbora da konstantea eta x kokagunea aldakorra.
u(x, t) perturbazioaren deribatua
t denborari buruz, x = cte. den puntu finko batean, t denborari buruzko u funtzioaren deribatu partziala da,
 hain zuzen; eta u(x, t)
perturbazioaren deribatu partziala x kokaguneari buruz, t aldagaia konstante dela,
hain zuzen; eta u(x, t)
perturbazioaren deribatu partziala x kokaguneari buruz, t aldagaia konstante dela,
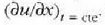 adierazten da.
adierazten da.
Lehenengo deribatuak u uhinak puntu jakin horretan duen lastertasuna ematen du, eta bigarrenak berriz, inguruneko puntuen arteko x distantzia banako bakoitzeko u(x, t) funtzioak duen aldakortasuna, hau da u(x, t) perturbazioaren aldakortasun "lastertasuna" x ardatzaren arabera (baina t unean, beti).
u(x, t) = A cos (la - bx) uhin laua deribatu partzialetan emandako ekuazio baten kasu partikularra da, lortzen erraza. Izan ere, u(x, t)funtzioa bi aldiz deribatzen bada t denborari buruz eta beste bi aldiz x kokaguneari buruz, emaitza hau ateratzen da:
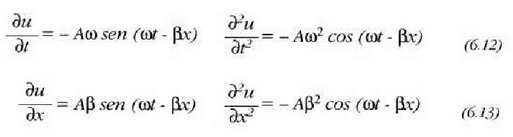
Aurreko adierazpenetatik abiatuta, eta kontuan harturik
 dela, orduan:
dela, orduan:

Ekuazio hori x eta t aldagaien mende dauden eta v lastertasunean hedatzen diren uhinek betetzen dute. Uhin lauaren ekuazio esaten zaio, eta garrantzi handiko hainbat gertaera fisiko aztertzeko erabili ohi da
Huygensen printzipioa
Uhin fronteak
Hiru dimentsioko u = u(x, y, z, t) uhin bat deskribatzeko ezinbestekoa da uhin frontea nola mugitzen den jakitea. Uhin frontea une jakin batean dardara fase berbera duten inguruneko puntu guztien toki geometrikoa da, definizioz. Uhin frontearen ondoz ondoko kokaguneen irudiak uhin mugimendua islatzen du. Ingurunea homogeneoa eta isotropoa bada, uhin frontearen normalaren norabide berean hedatuko da uhina beti. Puntu bakarreko fokuari buruz norabide guztietan hedatzen da uhina eta, horrenbestez, uhin frontea esfera itxurakoa da (6.9. a irudia). Uhin hauek esferaren zentrotik erradioetan zehar hedatzen dira, eta fokutik urrun daudenean, uhin frontearen gainaldeko elementu txikiak gainalde lautzat har daitezkeenez, uhin lau bat lortzen da (6.9 b irudia). Uhin lau baten uhin fronteak plano bat osatzen du, uhinaren normalaren norabidean hedatzen den plano bat hain zuzen. Uhinak igortzen dituen fokua lerro itxurakoa bada (6.9 c irudia), berriz, uhin zilindrikoa lortzen da, zilindroaren ardatzen erradioetan zehar hedatzen den uhin zilindriko bat.
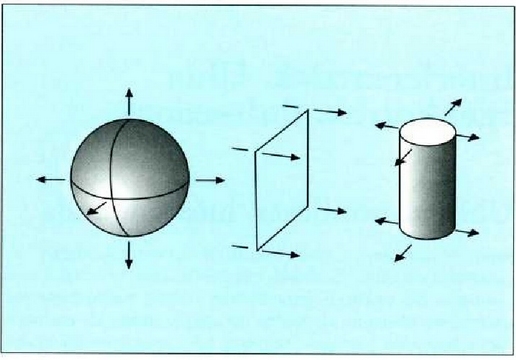
69: Uhin esferikoak, lauak eta zilindrikoak
Huygensen printzipioa
Huygensen printzipioak dio uhin fronte baten puntu orotatik uhin sekundarioak (uhin elementalak) ateratzen direla noranzko guztietarantz.
6.10 irudian Huygensen printzipioa aplikatu zaio uhin esferiko bati. Printzipio horren arabera, uhin fronte baten edozein puntu izandaiteke uhin elementalen abiapuntu. Bitez puntu bakarreko foku batetik ateratzen den uhin esferiko baten a, b, c... puntuak. Puntu horiek uhin elementalak igortzen dituzte, aldi berean, eta uhin horien gainalde inguratzaileak A, B, C... fronte berria osatuko du. Geroago uhin frontea L, M, N... izango da, eta horrela hurrenez hurren.
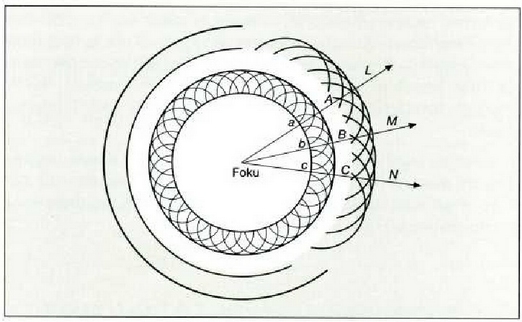
610: Uhin esferiko batean, puntu bakarreko fokutik ateratzen diren puntuek uhin elementalak igortzen dituzte, aldi berean; uhin elemental horien inguratzailea beste uhin fronte bat izango da.
Uhinen isla, Huygensen printzipioaren arabera
Uhin bat bi ingurune homogeneo baina ezaugarri optiko desberdineko bereizten dituen gainaldera iristen denean, gorabeherak gertatzen dira, oro har, uhin horren hedapen norabidean eta uhinaren gainaldean. Gertaera horri isla esaten zaio.
6.11 irudian, uhin batek I eta II bi inguruneren muga gainaldean duen uhin fronte lauaren zeharretarako epaia da AB. Baldin eta muga gainalde horrekin topo egin ez balu, uhinak aurrera jarraitukoko zukeen ordu arte zeraman norabide berean, eta denbora jakin bat igaro ondoren, uhinaren kokagunea CD izango litzateke. Baina muga gainaldeak uhin frontearen norabidea aldatzen du. Denbora tarte jakin batean B puntua D puntuari hurbiltzen zaio, eta A puntua ezin denez C puntura mugitu, lehen ingurunean egindako distantzia bera egiten du, eta AC erradioa duen CQ arkuko punturen batera iristen cia. Beste edozein E puntu inolako oztoporik gabe iristen da F puntura, eta ezin denez G punturaino iritsi, distantzia hera egiten du lehen ingurunean FG arkuaren punturen baten gainean. DH lerroa, arkuen ukitzaile dena, denbora tartea amaitzen denean uhin fronte izango denaren zeharretarako epaia da. AB lerroak uhin fronte jotzailea adierazen du, eta DH lerroak, islaturiko uhin frontea. Uhin horiek gainalde islatzailearekin eratzen dituzten f eta f" angeluak intzidentzia angelua eta isla angelua dira, hurrenez hurren.
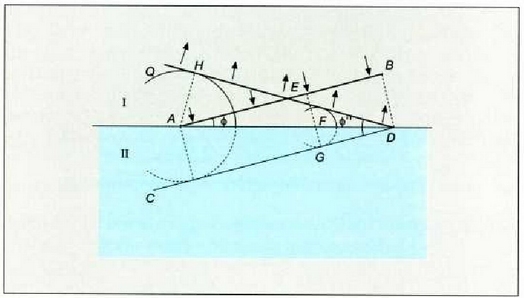
6 11: Isla legearen dedukzioa Huygensen printzipiotik abiatuta.
Intzidentzia angeluaren eta isla angeluaren arteko erlazioa erakusteko AH erradioa irudikatzen da H puntutik. Kontuan harturik DB = AC = AH dela, ADH eta DAB hiruki laukizuzenak berclinak izango dira. Horrenbestez,

Angelu horiek plano berean daude biak, A, B, D eta H angeluak ere plano berean baitaude. Azalpen hori ematen du, hain zuzen, isla legeak: uhin batek gainalde lau batjotzen duenean, islatu egiten da, eta intzidentzia angelua isla angeluaren baliokidea da. Bi angelu horiek plano berean daude
Uhinen errefrakzioa, Huygensen printzipioaren arabera
Bi inguruneren muga gainaldea jotzen duen uhin baten norabidea bat-batean aldatzen cia baldin eta bigarren ingurunean uhinak duen heclapen lastertasuna ez bada lehen ingurunean zuenaren berdina. Gertaera horri errefrakzio deritzo. 6.12 irudian, AB uhin fronte jotzailea, v lastertasuna duena, 0 intzidentzia angelua cluten bi inguruneren arteko muga gainaldean dago. Gainalde horretara iristen

6.12: Errefrakzio legearen dedukzioa Huygensen printzipiotik abiatuta
den argiaren parte bat lehenengo ingurunean islatzen da, eta beste parte bat bigarren ingurunean sartzen da. Eman dezagun bigarren ingurunean sartzen den argia bakarrik hartzen dela kontuan, eta v lastertasunean doala argi hori. B puntuak lehen ingurunean DB distantzia betetzeko behar duen denboran A puntuak ez clu AC distantzia betetzen bigarren ingurunean, baizik eta AH distantzia bat.
zentroa A duen arkuko punturen baten gainean. Baina, kontuan harturik

dela, bigarren adierazpena zati lehena egin eta berdintza hau ateratzen da:

Lehenengo ingurunean F punturainoko distantzia egiten duen beste edozein E puntuk (v'/v) FG
distantzia egiten du bigarren ingurunean, zentroa F puntuan duen arkuko punturen baten gainean.
DH lerroa, arku horien ukitzailea, denbora tartearen amaieran errefraktaturiko uhinaren frontea bera cia.
Muga gainaldearekin eratzen duen  angelua
errefrakzio angelua da.
angelua
errefrakzio angelua da.
Intzidentzia angeluaren eta errefrakzio angeluaren arteko erlazioa zein cien aurkitzeko AH erradioa irudikatzen cia H puntutik abiatuta. Orduan:
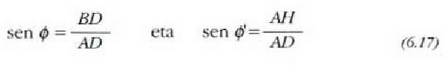
Horrenbestez,
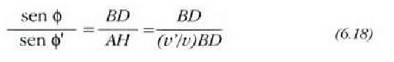
eta azkenik:

Erlazio horrek errefrakzio legea ematen du aditzera. Uhin bat bi inguruneren muga gainaldeari buruz zeharretara hedatzen denean, intzidentzia angeluaren sinuaren eta errefrakzio angeluaren sinuaren arteko arrazoiaren balioa eta ingurune bakoitzean uhinek dituzten lastertasunen arteko erlazioaren balioa berdinak dira. Intzidentzia eta errefrakzio angeluak plano berean daude.
Interferentziak. Uhin egonkorrak. Pultsazioak
Uhin armonikoen interferentzia
Ingurune jakin batean puntu bakoitzari aldi berean norabide eta noranzko bera tiuten bi uhinek eragiten badiote, eta uhin horiek maiztasun eta anplitude bera badute, orduan puntu batzuetan ondoriozko uhinaren anplitudea handiagoa izango cia eta beste puntu batzuetan txikiagoa. Gertaera honi interferentzia esaten zaio. Bitez
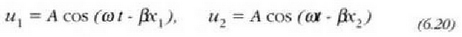
maiztasun eta anplitude bereko bi uhinen ekuazioak, bi uhinak x ardatzaren norabide positiboan
hedatzen direnean eta 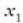 eta
eta  direlarik foku igorleek puntu jakin bati buruz duten distantzia.
direlarik foku igorleek puntu jakin bati buruz duten distantzia.
 egiten bada.
egiten bada.

Beraz:

Ondoriozko mugimendua, gainkatzearen printzipioaren arabera, uhin bakoizaren mugimenduaren batura izango da:

(6.23) ekuazioari  aplikatuz gero, adierazpen hau ateratzen da:
aplikatuz gero, adierazpen hau ateratzen da:
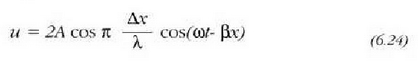
edo

Ekuazio hori uhin osagaien ezaugarri berberak dituen uhin bati dagokio (6.13 irud.), baina uhin honen anplitudea,

Ax aldagaiaren arabera aldatzen da. Anplitude gorena izango du

betetzen denean (anplitudearen balio absolutua bakarrik harturik). Eta hori x aldagiaren edozein baliorentzat

betetzen denean gertatuko da,
hau da 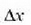 uhin luzeren kopurua
kopuru osoa denean. Anplitudea 2A izango da kasu horretan.
uhin luzeren kopurua
kopuru osoa denean. Anplitudea 2A izango da kasu horretan.
Aldiz, anplitudea baliogabea izango da x aldagaiaren edozein baliorentzat

betetzen denean, eta balio hauei dagokie kasu hori:
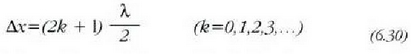
hau da uhin luzera erdien kopuru bakoitia dagokionean 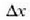 aldagaiari.
aldagaiari.

6.13: Maiztasun eta anplitude bera duten eta ia fBean dauden bi uhin elkarren gainean jartzean eratzen den uhinaren anplitudea bere edozein osagairen anplitudearen bikoitza da ia
Uhin egonkorrak
Bi kosinu uhin lauren interferentzia aztertuko da orain, uhin horiek anplitude eta maiztasun bera duten baina elkarren kontrako noranzkoan mugitzen diren kasurako. Bitez

x ardatzaren norabide positiboan hedatzen den uhinaren ekuazioa, eta

ardatz horren norabide negatiboan hedatzen den uhinaren ekua- zioa. Eman dezagun koordenatuen sorburuan (x = 0) bi uhinak fasean daudela t unean. Gainkatzearen printzipioaren arabera, bi sinu uhinen batura izango da ondoriozko uhina:

edo
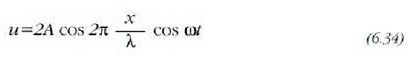
Ekuazio horrek ez du uhin mugimendu bat adierazten, x eta t aldagaiek ez baitute osatzen (x - vt) konbinazioa. Dardara mugimendu armoniko bati dagokio; mugimendu hori denboraren mendeko eragileak zehazten du, cos wt aldagaiak; bere anplitudea,

x koordenatuaren funtzio periodikoa da, eta x aldagaiari buruz askea du fasea, wt. (6.34) ekuazioa dagokien uhinei uhin egonkor esaten zaie.
(6.35) ekuazioaren arabera, ondoko berdintza betetzen duten puntuak dira anplitude handienekoak (anplitudearen balio absolutua bakarrik harturik kontuan):

Baldintza hori betetzen duten puntuei koordenatu hauek dagozkie:

Anplitudearen balioa 2A da kasu horretan. Horrela, badira uhin luzera erdi batez,
 , bereizitako puntu batzuk,
anplitude goreneko (2A) dardara mugimendu armonikoa egiten dutenak. Puntu horiei dardararen antinodo deritze.
Elkarren segidan dauden bi antinodoren arteko distantzia uhin luzeraren erdia da, hain zuzen,
, bereizitako puntu batzuk,
anplitude goreneko (2A) dardara mugimendu armonikoa egiten dutenak. Puntu horiei dardararen antinodo deritze.
Elkarren segidan dauden bi antinodoren arteko distantzia uhin luzeraren erdia da, hain zuzen,

Era berean,

ekuazioa betetzen denean, hau da

koordenatuak dagozkien puntuetan, anplitudea baliogabea cla. Puntu horiek geldik daude beti, eta nodo izena ematen zaie;
elkarren segidan dauden bi nodoren arteko distantzia  da.
(6.37) eta(6.39) ekuazioek aditzera ematen dutenez, nodo baten eta haren segidan dagoen
antinodo baten arteko distantzia ere
da.
(6.37) eta(6.39) ekuazioek aditzera ematen dutenez, nodo baten eta haren segidan dagoen
antinodo baten arteko distantzia ere 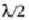 da.
(6.34) irudian uhin egonkor bat agertzen da grafikoki adierazia.
da.
(6.34) irudian uhin egonkor bat agertzen da grafikoki adierazia.

Uhin egonkorrak eta uhin mugikorrak bereizten dituzten ezaugarriak hauek dira:
a) uhin egonkor batean, dardaren anplitudea ez da berdina inguruneko toki guztietan; sistemak nodoak
eta antinodoak ditu; uhin mugikor batean, aldiz, anplitude murrizketarik gabe, anplitude bera dago toki guztietan;
b) uhin egonkor baten ondoz ondoko bi nodoren arteko puntuak fase berean dardaratzen dira;
uhin mugikor batean, oszilazioaren fasea  x ardatzaren mende dago; c) uhin egonkor batean ez dago energia
garraio aldebatekorik, eta uhin mugikorretan aldiz hati. Uhin
egonkorraren adierazpenak, beraz, ingurunea dardarei dagokienez
zein egoeretan dagoen ematen du aditzera.
x ardatzaren mende dago; c) uhin egonkor batean ez dago energia
garraio aldebatekorik, eta uhin mugikorretan aldiz hati. Uhin
egonkorraren adierazpenak, beraz, ingurunea dardarei dagokienez
zein egoeretan dagoen ematen du aditzera.
Pultsazioak
Uhinak zein bere lastertasunean hedatzen direnean, oro har, egoera ez periodiko bat gertatzen da, haina zaila da egoera horren bestelako ezaugarririk zehaztea. Hala ere, uhinen maiztasunak elkarren antzekoak direnean, gertaeraren nondik norakoa ezagutu daiteke. Kasurik soilena anplitude bereko bi oszilazio desberdin samarren kasua da; kasu horretan pultsazioek (batimentoek) modulaturiko oszilazioa eratzen dute bi oszilazioek. Dispertsioa dagoenean, hau da, uhin lastertasuna anplitudearen, maiztasunaren edo dardara motaren mende ez dagoenean, modulazioa uhin eramalearen lastertasun berean hedatzen da. Baina dispertsioa cagoenean, beste lastertasun bat dagokio, taldearen lastertasuna, hain zuzen.
A anplitude bera
(kalkulua errazagoa izan dadin) duten eta x ardatzaren norabide positiboan hedatzen diren bi uhin armoniko
lau harturik, eman dezagun lehen uhinak  maiztasun zirkularra duela eta
maiztasun zirkularra duela eta 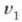 lastertasunean mugitzen dela, eta bigarren uhinaren maiztasun zirkularra
lastertasunean mugitzen dela, eta bigarren uhinaren maiztasun zirkularra
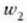 dela eta lastertasuna
dela eta lastertasuna
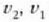 lastertasunaren desherdina.
lastertasunaren desherdina.
Bitez bi uhin horien ekuazioak:

Ondoriozko uhina bi uhinak elkarren gainean jarririk lortzen dena da. Beraz:
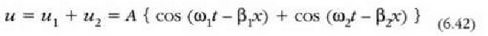
Adierazpen hori soiltzeko ondoko aldaketa hauek egin daitezke:
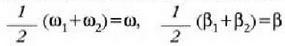
batez besteko balioentzat eta

batez bestekoen diferentziarentzat.
Orduan heste era honetan idatzi ahal izango da (6.42) ekuazioa:

edo,

non
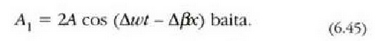
(6.43) ekuazioa w maiztasun zirkularreko eta  uhin luzerakouhin lau bati dagokio; uhin hori x ardatzaren norabide positiboan
hedatzen da. Ez du anplitude konstantea, denboraren eta kokagunearen
arabera aldatu egiten baita pixkanaka, 2A eta 0 balioen artean;
portaera horrekin pultsazio izeneko gertaera eragiten du.
Beraz, anplitude modulatuko uhin mugimendu bat da.
uhin luzerakouhin lau bati dagokio; uhin hori x ardatzaren norabide positiboan
hedatzen da. Ez du anplitude konstantea, denboraren eta kokagunearen
arabera aldatu egiten baita pixkanaka, 2A eta 0 balioen artean;
portaera horrekin pultsazio izeneko gertaera eragiten du.
Beraz, anplitude modulatuko uhin mugimendu bat da.
6.15 irudian A = A cos (wt - bx) uhinaren adierazpen
grafikoa egin da, eta 6.16 irudian, berriz,  anplitude modulatuko uhina (a kurba) eta
anplitude modulatuko uhina (a kurba) eta  uhina (b kurba) marraztu dira.
uhina (b kurba) marraztu dira.
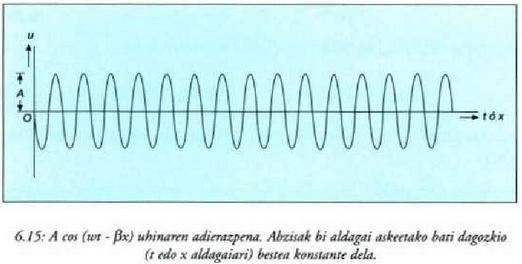
Abzisak bi aldagai askeetako bati dagozkio (t edo x), beste aldagaia konstante dela.
Azpimarratzekoa da anplitudea ez dela hedatzen uhinaren lastertasun berean.
Uhina  fase
lastertasunean hedatzen da.
fase
lastertasunean hedatzen da.
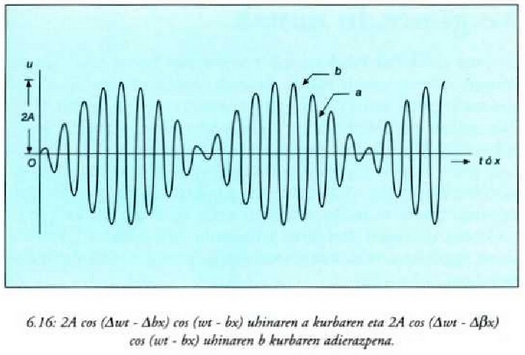
Anplitudea zein lastertasunetan hedatzen den jakiteko, argumentuak konstante izan behar du:

Anplitude konstanteko planoak, beraz,

lastertasunean hedatzen dira. Adierazpen horretan taldearen lastertasuna da
 aldagaia,
eta uhin inguratzailearen fase lastertasuna ematen du aditzera.
aldagaia,
eta uhin inguratzailearen fase lastertasuna ematen du aditzera.
Demagun, 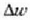 aldagaia txikia dela eta
aldagaia txikia dela eta
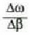 adierazpenaren ordez
adierazpenaren ordez
 jar daitekeela.
Kasu horretan
jar daitekeela.
Kasu horretan

da taldearen lastertasuna.
Kontuan harturik  dela,
aurreko ekuazioan ordezkatuz, beste ekuazio hau aterako da:
dela,
aurreko ekuazioan ordezkatuz, beste ekuazio hau aterako da:
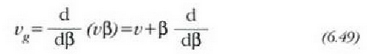
Hau da,

Ekuazio horrek taldearen lastertasuna neurtzeko fase lastertasuna erabiltzeko aukera ematen du.
Baldin eta dispertsiorik ez badago, hau da, fase lastertasuna
T (edo  ) aldagaiaren mende ez badago, orduan
) aldagaiaren mende ez badago, orduan
 eta
eta
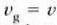 beteko da, hau da,
taldearen lastertasuna fase lastertasunaren berdina izango da.
beteko da, hau da,
taldearen lastertasuna fase lastertasunaren berdina izango da.
Fase lastertasunaren eta taldearen lastertasunaren kontzeptuek garrantzi handia dute fisika modernoan. Uhinen mekanikaren arabera, mugitzen den zatiki bat uhin talde bat da, eta haren lastertasuna taldearen lastertasuna da. Taldea osatzen duten uhinak argiaren lastertasuna baino fase lastertasun bizkorragoan hedatzen dira, eta taldearen lastertasuna, aldiz, geldiroago hedatzen da; gertaera hori erlatibitatearen teoriarekin bat dator.
Adibidea. Uhin jakin baten fase lastertasuna 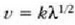 formularen bidez adierazten da, formula horretan k aldagaia konstante dela. Zehaztu talde lastertasuna.
formularen bidez adierazten da, formula horretan k aldagaia konstante dela. Zehaztu talde lastertasuna.
Ebazpena. (6.50) ekuaziotik, kontuan harturik  dela,
ondoko adierazpen hau ateratzen da:
dela,
ondoko adierazpen hau ateratzen da:
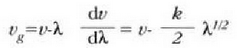
Beraz:
 edo
edo

hau da, talde lastertasuna fase lastertasunaren erdia da hain zuzen ere.
7. Gorputz gotor zurrunak
Gorputz gotor zurrunaren zinematika
Sarrera
Jakina denez, gorputz gotor zurruna materia sistema bat da, bere zatikien arteko
distantzietan bat ere aldaketarik ez daukana. Gorputz horien mugimendua aztertzeko,
beren posizioa eta orientazioa jakin beharra dago; horretarako gorputz gotor horretako
hiru puntu lerrokatugabe hartu behar dira, edozein,
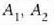 eta
eta
 , eta haien posizio
bektoreak ezagutu behar dira
, eta haien posizio
bektoreak ezagutu behar dira 
 eta
eta
 (7.1 irudia).
Baina hiru puntu horien arteko distantziek aldaketarik ez dutenez, hiru puntu horiek definitzen
dituzten bederatzi koordenatu kartesiarrak ez dira elkarrekiko independenteak, ekuazio eskalar hauen bidez
baitaude elkarrekin erlazionatuta:
(7.1 irudia).
Baina hiru puntu horien arteko distantziek aldaketarik ez dutenez, hiru puntu horiek definitzen
dituzten bederatzi koordenatu kartesiarrak ez dira elkarrekiko independenteak, ekuazio eskalar hauen bidez
baitaude elkarrekin erlazionatuta:

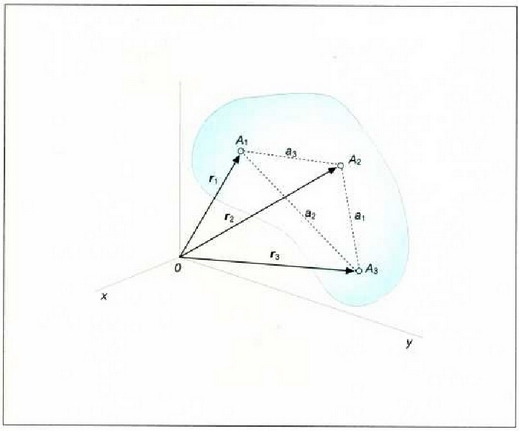
7.1: Gorputz gotor zurrun baten posizioa erabat definitzeko, gorputz horretako hiru puntu lerrokatugabe, edozein, hartu behar dira, eta haien posizio bektoreak ezagutu behar dira.
Baina, ekuazio horien bidez bederatzi koordenatuetatik hiru kalkulatu ahal izango baitira beti, sei baizik ez dira izango gorputz gotor zurrun horrek espazioan duen posizioa eta orientazioa erabat definitzeko behar diren aldagai independenteak. Gertaera hori adierazteko, sistema horrek askatasunezko sei gradu dituela esaten da
Mugimendu motak
Gorputz gotor bat erreferentzia sistema bati buruz mugitzen ari denean, bere puntuek egiten dituzten ibilbideek lastertasun eta azelerazio jakin batzuk dituzte. Gorputz hori mugitzen ari den bitartean, gorputz horretako bi puntu, edozein, lotzen dituen edozein bektore bektore horren beraren paralelo mugitzen denean, gorputz gotor horrek egiten duen mugimenduari translazio mugimendua esaten zaio (7.2 irudia); eta gorputz hori mugitzen ari den bitartean horko bi puntu, edozein, finko gelditzen badira, puntu horietatik igarotzen den lerro zuzenaren -errotazio ardatza du izena- inguruko errotazioa esaten zaio gorputz gotor horren mugimenduari (7.3 irudia).

72: Gorputz gotor zurrun batek translazio mugimendu bat egiten du gorputzaren bi puntu, edozein, lotzen dituen bektorea berari buruz paraleloan lekualdatzen denean.

73: Gorputz gotor zurrun batek errotazio mugimendu bat egiten du gorputz horretako bi puntu, edozein, mugimenduak irauten duen bitartean finko gelditzen direnean.
Translazio mugimendua
Demagun translazio mugimendu bat egiten ari den gorputz gotor zurrun bat,
eta har ditzagun gorputz horretako bi puntu, edozein, A eta B (7.4 irudia).
Baldin eta 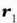 eta
eta  badira puntu horien
posizio bektoreak Oxvz erreferentzia sistema finko bati buruz, eta r baldin badaA eta B puntuak lotzen
dituen bektorea, orduan
badira puntu horien
posizio bektoreak Oxvz erreferentzia sistema finko bati buruz, eta r baldin badaA eta B puntuak lotzen
dituen bektorea, orduan

Gorputz gotorraren translazio mugimenduan r bektorea konstantea denez magnitudez, norabidez eta noranzkoz, B puntuaren ibilbidea A puntuaren ibilbidetik ateratzen da, bere puntu guztiak rbektorearen moduluaren luzera berdinean paraleloan lekualdatzen dituela. Beraz,
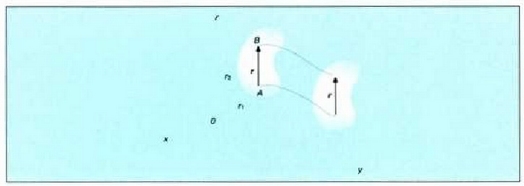
74: Translazio mugimendua egiten ari den gorputz gotor zurrun bateko puntu guztiek ibilbide berdinak egiten dituzte
Translazio mugimenduan, gorputzgotor horretako puntu guztiek ibilbide berdinak egiten dituzte. Gorputz horren puntu baten ibilbidea ezagutuz gero (masen zentroarena, aclibidez), aise jakin claiteke beste puntu guztien ibilbidea zein den.
(7.2) ekuazioa denborari buruz deribatuz A eta B puntuen ibilbidea ateratzen da. Hau da emaitza:
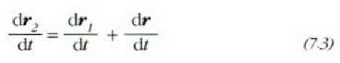
eta dr/dt=O denez, hau ateratzen da:

alegia, translazio mugimendu batean gorputz gotor horretako puntu guztiek lastertasun bera dute momentu berean. v lastertasunari, gorputz horretako puntu guztiek komun tiuten lastertasunari, alegia, gorputz horren translazio mugimenduaren lastertasuna esaten zaio (7.5 irudia).
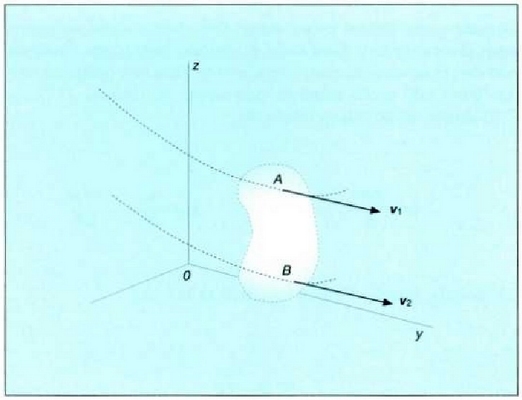
75: Translazio mugimendua egiten ari den gorputz gotor zurrun bateko puntu guztiek lastertasun bera dute momentu berean
A eta B puntuen azelerazioa (7.4) ekuazioa berriz deribatuz jakiten da:
 edo bestela
edo bestela 
alegia, translazio mugimendu batean, gorputz gotor horretako puntu guztiek azelerazio berdrnak dituzte inomentu berean (7.6 irudia). a azelerazioari, gorputz gotor horretako solido guztiek komun dutenari, gorputz horren translazio mugimencluaren azelerazioa esaten zaio. v eta a bektoreak gorputzaren edozein punturi aplika dakizkioke. Gorputz gotorraren lastertasuna eta azelerazioa aclierek esanahi bat dute translaziozko mugimenduan. Espazioan libre lekualdatzen cten gorputz gotor bateko puntuek lastertasun eta azelerazio desberdinak dituzte oro har.

7.G- Translazio mugimendu bat egiten ari den gorputz gotor bateko puntu guztiek azelerazio bera dute momentu berean
Errotazio mugimendua ardatz finko baten inguruan. Angelu lastertasuna eta azelerazioa
Gorputz gotor bat zz' ardatz finko baten inguruan biraka ari denean, gorputz gotor horretako puntu bakoitzak A zirkunferentzia egiten du ardatzarekin normala cien planoan; zirkunferentzia horrek errotazio ardatzean dauka erdigunea, eta erdigune hori orobat da A puntuak ardatzaren gainean egiten duen B proiekzioa; puntutik ardatzera dagoen AB distantzia du zirkunferentzia horrek erradioa (7.7 irudia).
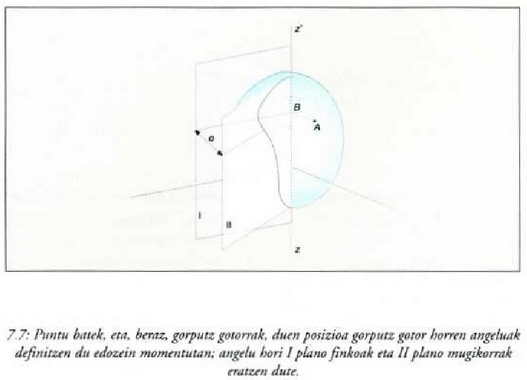
Errotazioan dagoen gorputz gotorrak duen posizioa definitzeko, ardatz horretatik igarotzen diren bi plano hartu behar dira kontuan: I plano finkoa eta 11 planoa, gorputz gotorrari atxikia, eta gorputzarekin batera biraka ari dena. Angelu horri gorputz gotorraren errotazio angelua (edo angelu koordenatuak) esaten zaio. F angelua positibotzat hartzen da I planotik erlojuaren orratzen kontrako noranzkoan neurtzen bada, eta negatibotzat, berriz, erlojuaren orratzen noranzko berean neurtzen denean. F angelua radianetan adierazten da.
Gorputz horrek edozein momentutan duen posizioa definitzeko, gorputz gotorraren mugimenduaren legea jakin beharra dago; alegia,

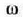 angelu lastertasuna eta
angelu lastertasuna eta  angelu azelerazioa dira gorputz gotor baten errotazio mugimenduaren ezaugarri nagusiak.
angelu azelerazioa dira gorputz gotor baten errotazio mugimenduaren ezaugarri nagusiak.
Angelu lastertasuna.
Ekuazio honek definitzen du  bektorea:
bektorea:

ekuazio horretan errotazio ardatzaren luzera osoan eta norabidean dagoen banako bektore bat da k,
eta gorputz horren angelu lastertasun une batekoa esaten zaio. Bektore horren modulua,
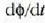 , eta errotazio angeluaren
deribatua denborari buruz berdinak dira; errotazio ardatzaren norabide bera du, eta noranzkoa halako modukoa du,
non gorputz gotorrak ardatzaren inguruan egiten duen errotazioa gorputzarekin batera biraka dabilen torloju batek
sartzen denean duen noranzkoari baitagokio. Definizio horren arabera,
, eta errotazio angeluaren
deribatua denborari buruz berdinak dira; errotazio ardatzaren norabide bera du, eta noranzkoa halako modukoa du,
non gorputz gotorrak ardatzaren inguruan egiten duen errotazioa gorputzarekin batera biraka dabilen torloju batek
sartzen denean duen noranzkoari baitagokio. Definizio horren arabera,
 bektorea bektore lerragarria da, haren sorburua modu arbitrarioan aukera baitaiteke errotazio ardatzaren gainean.
bektorea bektore lerragarria da, haren sorburua modu arbitrarioan aukera baitaiteke errotazio ardatzaren gainean.
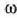 zeinuak gorputzaren
errotazioaren noranzkoa definitzen du. Une jakin batean
zeinuak gorputzaren
errotazioaren noranzkoa definitzen du. Une jakin batean
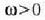 denean, errotazioak
erlojuaren orratzen kontrako noranzkoa du, eta
denean, errotazioak
erlojuaren orratzen kontrako noranzkoa du, eta 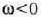 denean, errotazioak erlojuaren orratzen noranzko bera du. Angelu lastertasuna radian
denean, errotazioak erlojuaren orratzen noranzko bera du. Angelu lastertasuna radian
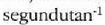 adierazten da.
adierazten da.
Angelu azelerazioa. Gorputz gotor baten angelu azelerazioak angelu lastertasunak denboraren arabera duen aldaketa definitzen du. a bektorea ekuazio honek definitzen du:

eta bektore horrigorputzaren angelu azelerazio une batekoa esaten zaio. Bektore horren modulua,
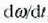 , eta errotazio
angeluaren bigarren deribatua denborari buruz,
, eta errotazio
angeluaren bigarren deribatua denborari buruz, 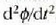 ,
berdinak dira; errotazio ardartzaren norabide berbera du, eta
,
berdinak dira; errotazio ardartzaren norabide berbera du, eta
 -ren noranzko berbera orobat,
angelu lastertasunaren modulua denboraren arabera gehitzen denean (7.8 irudia). Angelu lastertasunaren modulua
denboraren arabera gutxitzen baldin bada, orduan
-ren noranzko berbera orobat,
angelu lastertasunaren modulua denboraren arabera gehitzen denean (7.8 irudia). Angelu lastertasunaren modulua
denboraren arabera gutxitzen baldin bada, orduan  kontrako noranzkoa du (7.9 irudia). Angelu azelerazioa radian
kontrako noranzkoa du (7.9 irudia). Angelu azelerazioa radian
 neurtzen da.
neurtzen da.
78: Gorputzaren errotazio mugimendua azeleratzen denean, angelu azelerazioak eta angelu lastertasunak noranzko berbera dute
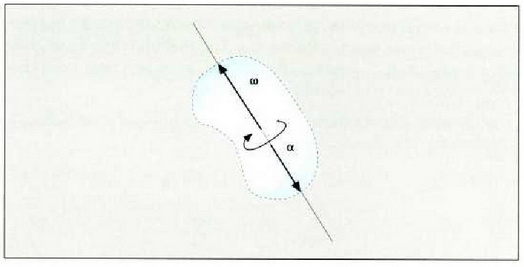
79. Gorputzaren errotazio mugimendua moteltzen denean, angelu azelerazioak eta angelu lastertasunak kontrako noranzkoa dute
Gorputz gotor zurrun batek ardatz finko baten inguruan egiten duen errotazio mugimendua definitzen duten ekuazioak
Gorputz gotor zurrun batek ardatz finko baten inguruan egiten duen errotazioa definituta dago
 angelua denboraren
funtzioan zein den ezagutzen denean, alegia,
angelua denboraren
funtzioan zein den ezagutzen denean, alegia, 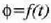 .
Hala ere, praktikan,
.
Hala ere, praktikan, 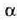 t- ren,
t- ren,
 -ren edo
-ren edo
 -ren funtzioan adierazten da.
Orduan, (7.7) eta (7.8) ekuazioetatik hau ateratzen da:
-ren funtzioan adierazten da.
Orduan, (7.7) eta (7.8) ekuazioetatik hau ateratzen da:
 eta
eta
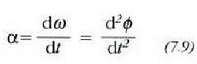
edo bestela, aurreko ekuazio horietatik dt kenduz:

Ekuazio horiek integratuz mugimendua defini daiteke.
Kasu bereziak:
a) a=0 baldin bada, mugimenduak errotazio uniformea du,  konstantea da, eta
konstantea da, eta 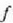 angelua formula honen bidez definituko da:
angelua formula honen bidez definituko da:

b) a=konstantea baldin bada, errotazioak azelerazio uniformea du, orduan:

 -ren eta a-ren
balioek zeinu bera dutenean, errotazioak azelerazio uniformea du; zeinuak desberdinak direnean,
errotazioak moteltze uniformea du.
-ren eta a-ren
balioek zeinu bera dutenean, errotazioak azelerazio uniformea du; zeinuak desberdinak direnean,
errotazioak moteltze uniformea du.
Puntuaren mugimendu zuzenaren legearen eta aztertu berri den gorputz gotor zurrunaren errotazio mugimenduaren legearen artean analogia formala dagoenez, korrespondentzia hauek egin daitezke:
x (lekualdatze zuzena)  (angelu lekualdatzea)v (lastertasun zuzena)
(angelu lekualdatzea)v (lastertasun zuzena)
 (angelu lastertasuna)a (azelerazio zuzena)
(angelu lastertasuna)a (azelerazio zuzena)
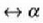 (angelu azelerazioa).
(angelu azelerazioa).
Adibidea. Gorputz baten angelu lastertasunak
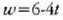 da, non w rad
da, non w rad
 tan adierazten baita, eta t segundutan.
Gauza jakina da t=O denean,
tan adierazten baita, eta t segundutan.
Gauza jakina da t=O denean, 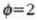 radian.
Kalkulatu
radian.
Kalkulatu  zenbat balio duen t=10 segundu denean.
zenbat balio duen t=10 segundu denean.
Ebazpena.  denez, ekuazio hau ateratzen da:
denez, ekuazio hau ateratzen da:
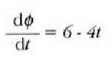
Beraz:
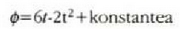
Baina, t=0,  rad. denez,
orduan konstantea=2. Beraz,
rad. denez,
orduan konstantea=2. Beraz,
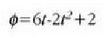
eta t=10 segundu denean, orduan
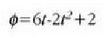
Lastertasun zuzena angelu lastertasunaren arabera
Demagun A gorputz gotor zurrun bateko puntu arbitrario bat dela ardatz finko batean gainean hiraka ari dena (7.10 irudia). r bektoreak definitzen du puntu horren posizioa; bektore horrek errotazio ardatzeko O puntu arbitrario eta, beraz, gorputz gotorrari hurrefinko batean du sorburua. Orain frogatuko da puntu horren v lastertasuna ekuazio honen berdina dela

ekuazio horretan  gorputzaren angelu lastertasuna adierazten du. Izan ere, v-ren modulua honela definitzen da:
gorputzaren angelu lastertasuna adierazten du. Izan ere, v-ren modulua honela definitzen da:

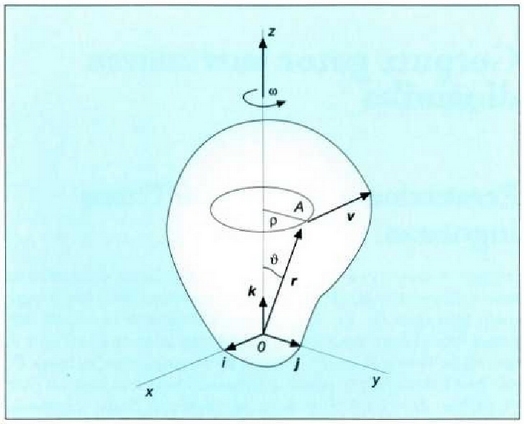
710: Gorputz bateko puntu arbitrario baten lastertasun zuzena bektorea eta gorputz gotor horren angelu lastertasuna puntu jakin horren erradio bektoreaz biderkatzetik ateratzen den emaitza berdinak dira
modulu horren norabidea r-k eta 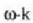 definitzen duten planoari buruz elkarzuta da, eta haren noranzkoa gorputzarekin batera biraka ari den
torlojuak sartzen denean duen noranzkoari dagokio. Beraz, gorputz bateko puntu arbitrario baten lastertasun
zuzena bektorea eta gorputz gotor horren angelu lastertasuna puntu jakin horren erradio bektoreaz biderkatzetik
ateratzen den emaitza berdinak dira.
definitzen duten planoari buruz elkarzuta da, eta haren noranzkoa gorputzarekin batera biraka ari den
torlojuak sartzen denean duen noranzkoari dagokio. Beraz, gorputz bateko puntu arbitrario baten lastertasun
zuzena bektorea eta gorputz gotor horren angelu lastertasuna puntu jakin horren erradio bektoreaz biderkatzetik
ateratzen den emaitza berdinak dira.
Adibidea. Gorputz zurrun bat era berean ari da biraka koordenatu
laukizuzenen sistema baten sorburutik igarotzen den ardatz
baten inguruan, eta koordenatu sistema horrek angelu berdinak
eratzen ditu ardatz bakoitzarekin. Asmatu 3 metroko abzisa duenx ardatzaren gainean dagoen A puntu baten lastertasun lineala,
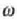 angelu lastertasuna
angelu lastertasuna
 dela jakinik.
dela jakinik.
Ebazpena. 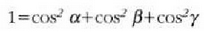 eta
eta
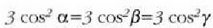 denez,
denez,
orduan:

Baina,  denez,
denez,
(7.13) ekuazioa aplikatuz hau ateratzen da:
eta  denez, eta x=3 metroa, ekuazio hau ateratzen da:
denez, eta x=3 metroa, ekuazio hau ateratzen da:

Eta j-k bektorearen norabide eta noranzko berbera izango ditu.
Gorputz gotor zurrunaren dinamika
Errotazioa ardatz finko baten inguruan
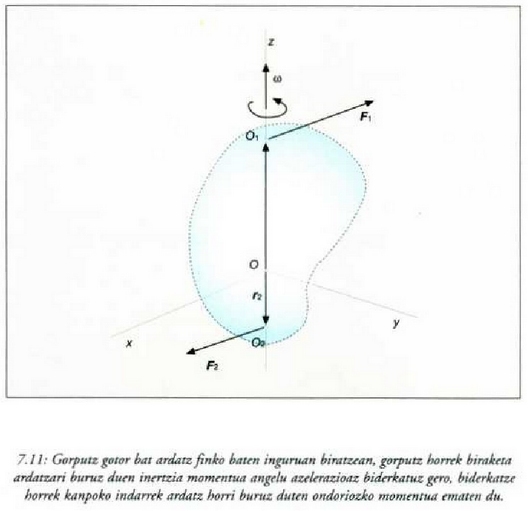
Gorputz zurrun batek Gorputz gotor zurrun baten errotazioaren kasu soilena aztertuko cla
orain, errotazioa ardatz finko baten inguruan. Demagun
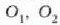 (7.11 irudia) puntuetatik
igarotzen den ardatz finko baten inguruan biraka ari den gorputz gotor zurrun bat. Puntu horiek
(7.11 irudia) puntuetatik
igarotzen den ardatz finko baten inguruan biraka ari den gorputz gotor zurrun bat. Puntu horiek
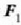 eta
eta
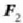 erreakzioak eragingo dituzte,
batek O, puntuan eta besteak
erreakzioak eragingo dituzte,
batek O, puntuan eta besteak  puntuan. Erreakzio horiek ez dira, oro har, ezagutzen.
puntuan. Erreakzio horiek ez dira, oro har, ezagutzen.  baldin bada kanpoko indarren (indar eragileen) ondoriozko momentua errotazio ardatzeko 0 puntu finko
bati buruz -puntu hori hartuko dela koordenatu kartesiarren sistema baten sorburutzat-, orduan, angelu momentuaren
teoremaren arahera, ekuazio hau aterako da:
baldin bada kanpoko indarren (indar eragileen) ondoriozko momentua errotazio ardatzeko 0 puntu finko
bati buruz -puntu hori hartuko dela koordenatu kartesiarren sistema baten sorburutzat-, orduan, angelu momentuaren
teoremaren arahera, ekuazio hau aterako da:
ekuazio horretan  , puntuen posizio bektoreak dira
0 puntuari buruz, eta
, puntuen posizio bektoreak dira
0 puntuari buruz, eta 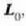 berriz,
gorputz gotor horren angelu
berriz,
gorputz gotor horren angelu

momentua, hori ere 0 puntuari buruz. 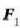 eta
eta 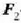 -ren erreakzio ezezagun horiek ezabatzeko,
(7.15) ekuazioaren eta z ardatzaren norabide eta noranzko bera cluen k banako bektorearen biderkaketa eskalarra egin beharra dago.
Orduan:
-ren erreakzio ezezagun horiek ezabatzeko,
(7.15) ekuazioaren eta z ardatzaren norabide eta noranzko bera cluen k banako bektorearen biderkaketa eskalarra egin beharra dago.
Orduan:
Baina  biderkaketak angelu
momentuaren
biderkaketak angelu
momentuaren  osagaia adierazten du
osagaia adierazten du

 errotazio ardatzaren norabidean,
eta
errotazio ardatzaren norabidean,
eta 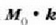 biderkaketak, berriz,
kanpoko indarren ondoriozko momentuaren
biderkaketak, berriz,
kanpoko indarren ondoriozko momentuaren 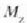 osagaia z ardatz horri buruz. Bi momentu horiek ez claude 0 puntuaren mende, baina hai hartu den errotaria
ardatzaren mende. (7.16) ekuazioa honela idatz daiteke beraz:
osagaia z ardatz horri buruz. Bi momentu horiek ez claude 0 puntuaren mende, baina hai hartu den errotaria
ardatzaren mende. (7.16) ekuazioa honela idatz daiteke beraz:

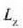 kalkulatzeko, har dezagun
masatzat dm duen gorputz gotor zurruneko gorpuzki puntu bat. 0 koordenatuen sorburutik puntu jakin
horretara dihoan r bektoreak definitzen du bere posizioa. Orduan, hau izango da zatiki horren angelu momentua:
kalkulatzeko, har dezagun
masatzat dm duen gorputz gotor zurruneko gorpuzki puntu bat. 0 koordenatuen sorburutik puntu jakin
horretara dihoan r bektoreak definitzen du bere posizioa. Orduan, hau izango da zatiki horren angelu momentua:

Baina  denez, non
denez, non
 gorputz horren angelu
lastertasuna adierazten baitu, orduan:
gorputz horren angelu
lastertasuna adierazten baitu, orduan:
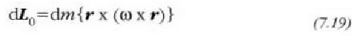
eta (1.75) ekuazioaren arabera, hau denez

hau ateratzen da:
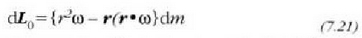
Beraz,  , gorputz gotorraren
angelu momentua zein den jakiteko, hau ateratzen da:
, gorputz gotorraren
angelu momentua zein den jakiteko, hau ateratzen da:

eta ekuazio horrek angelu momentua ematen du angelu lastertasunaren arabera.

non, x, v z, puntu jakin baten koordenatuak baitira, eta beraz:

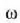 faktorea dm-tik independentea denez, aurreko ekuazioko bigarren osagaiko lehenengo terminoko zeinu integraletik
kanpora atera claiteke. Ekuazio hau ateratzen da orduan:
faktorea dm-tik independentea denez, aurreko ekuazioko bigarren osagaiko lehenengo terminoko zeinu integraletik
kanpora atera claiteke. Ekuazio hau ateratzen da orduan:
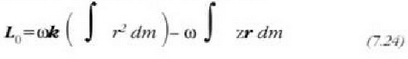
Beraz, angelu momentua ez da izaten, oro har, errotazio ardatzaren paraleloa.
Angelu momentuak errotazio ardatzaren norabidean duen osagaia zein den jakiteko, (7.24) ekuazioaren eta k-ren biderkadura eskalarra egin behar da:
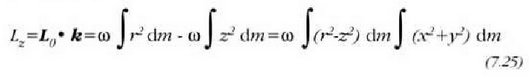
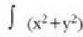 magnitude eskalarrari gorputz zurrunak errotazio ardatzariburuz (kasu honetan
magnitude eskalarrari gorputz zurrunak errotazio ardatzariburuz (kasu honetan
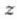 ardartzari buruz)
duen inertzia momentua esaten zaio, eta
ardartzari buruz)
duen inertzia momentua esaten zaio, eta 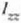 zeinuaren bidez adierazten da (Ohar bedi
zeinuaren bidez adierazten da (Ohar bedi 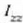 errotazio ardatzeko O puntuko posizioa independentea dela
errotazio ardatzeko O puntuko posizioa independentea dela
 inertzia momentutik;
ardatz horrek gorputzean duen posizioaren mende baizik ez clago). Beraz, (7.25) formulatik formula hau ateratzen da:
inertzia momentutik;
ardatz horrek gorputzean duen posizioaren mende baizik ez clago). Beraz, (7.25) formulatik formula hau ateratzen da:

Beraz, errotazio ardatzari buruz errotazioan ari clen gorputz gotor batean, gorputz horrek ardatz horri buruz duen inertzia momentua gorputz horren angelu lastertasunaz biderkatuz gero, biderkadura horrek angelu momentua ematen du.
Badago frogatzea  bektorea errotazio ardatzaren paraleloa dela, O puntuari dagokion
bektorea errotazio ardatzaren paraleloa dela, O puntuari dagokion
 ardatza simetriazko ardatz bat baldin bada. (7.26) ekuazio eskalarraren ordez beste ekuazio hau aterako litzateke orduan:
ardatza simetriazko ardatz bat baldin bada. (7.26) ekuazio eskalarraren ordez beste ekuazio hau aterako litzateke orduan:
 , eta ekuazio horretan
, eta ekuazio horretan
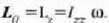
(7.26) ekuazioa deribatzen bada denborari buruz, eta (7.17) ekuazioa kontuan hartzen bada, ekuazio hau ateratzen da:
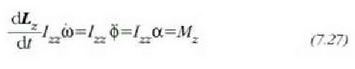
ekuazio horretan 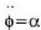 angelu azelerazioa da. (7.27) ekuazioak gorputz gotor zurrun batek ardatz finko baten inguruan egiten
duen errotazio mugimenduaren ekuazio diferentziala adierazten du, eta hau adierazten du: gorputz
horrek errotazio ardatzari buruz duen inertzia momentua angelu azelerazioaz biderkatuz gero,
biderkatze horrek kanpoko indarrek ardatz horri buruz duten ondoriozko momentua ematen du. (7.27)
ekuazioak hau erakusten du baita ere:
angelu azelerazioa da. (7.27) ekuazioak gorputz gotor zurrun batek ardatz finko baten inguruan egiten
duen errotazio mugimenduaren ekuazio diferentziala adierazten du, eta hau adierazten du: gorputz
horrek errotazio ardatzari buruz duen inertzia momentua angelu azelerazioaz biderkatuz gero,
biderkatze horrek kanpoko indarrek ardatz horri buruz duten ondoriozko momentua ematen du. (7.27)
ekuazioak hau erakusten du baita ere: 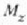 -rentzat
balio bat emanik, gorputzaren inertzia momentua zenbat eta handiagoa,
angelu azelerazioa orduan eta txikiagoa da, eta alderantziz.
Gorputzaren errotazio mugimenduan, masak translazio mugimenduan duen zeregin bera du inertzia mugimenduak ere;
alegia, errotazio mugimenduan inertzia momentua gorputzaren inertziaren neurria da.
-rentzat
balio bat emanik, gorputzaren inertzia momentua zenbat eta handiagoa,
angelu azelerazioa orduan eta txikiagoa da, eta alderantziz.
Gorputzaren errotazio mugimenduan, masak translazio mugimenduan duen zeregin bera du inertzia mugimenduak ere;
alegia, errotazio mugimenduan inertzia momentua gorputzaren inertziaren neurria da.
(7.27) ekuazioa integratuz gero,
ondorio hau ateratzen da: 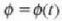 , alegia,
gorputzaren errotazio legea, edo gorputz horren angelu lastertasuna,
, alegia,
gorputzaren errotazio legea, edo gorputz horren angelu lastertasuna,
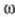 , ateratzen da,
baldin eta
, ateratzen da,
baldin eta  eta hasierako
baldintzak ezagutzen badira. Alderantziz,
eta hasierako
baldintzak ezagutzen badira. Alderantziz,  ezagutzen baldin bada,
ezagutzen baldin bada, 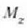 defini daiteke.
defini daiteke.
Kasu bereziak.  baldin bada, orduan
baldin bada, orduan
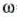 =konstantea, alegia, gorputzak
errotazio mugimendu uniforme bat egiten du, eta
=konstantea, alegia, gorputzak
errotazio mugimendu uniforme bat egiten du, eta  =konstantea baldin bada, orduan a=konstantea, alegia, gorputz horrek berdin azeleratutako errotazio mugimendu bat egiten du.
=konstantea baldin bada, orduan a=konstantea, alegia, gorputz horrek berdin azeleratutako errotazio mugimendu bat egiten du.
(7.27) formularen etaF=ma berdintzaren arteko forma analogiatik, zatiki batek lerro zuzen batean zehar egiten duen mugimenduari clagokiona hain zuzen, korrespondentzia hauek ateratzen dira:

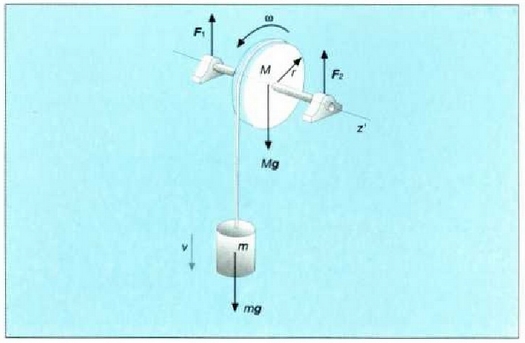
Horregatik, (7.27) ekuazioa integratzeko metodoak eta F=ma ekuazioa integratzeko erabili direnak berdin-berdinak dira. Bere ardatzaren inguruan aske bira daitekeen zilindro batek M du masa eta r erradioa; zilindro horrek hari du biribildua, eta hari horretatik zintzilik masa m duen gorputz bat dago zintzilik.
Adibidea.
1. Bere ardatzaren inguruan
aske bira daitekeen zilindro batek M du masa eta r erradioa; zilindro horrek hari bat du biribildua, eta hari
horretatik zintzilik masa ni duen gorputz bat dago zintzilik. Gorputz hori erortzen utziz gero, asmatu zein
den zilindro horren angelu azelerazioa. Ez dira kontuan hartu bhhar ez hariaren masa eta ez ardatzaren gaineko
marruskadura. 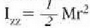 da zilindro horrek
errotazio ardatzari buruz duen inertzia momentua.
da zilindro horrek
errotazio ardatzari buruz duen inertzia momentua.
Ebazpena. Sistema honetan gorputz hatek errotaziozko mugimendu
bat egiten du eta beste gorputz batek traslaziozko mugimendu bat egiten du (7.12 irudia). Sistema horretan
kanpoko indar hauek dute eragina: diskoaren pisuak, Mg, gorputzaren pisua, mg, eta euskarrien
 eta
eta
 erreakzioak.
erreakzioak.
Angelu momentuaren teorema (7.27 ekuazioa) aplikatuz gero, ekuazio hau ateratzen da:
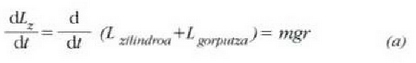
(Diskoaren pisuaren momentua eta erreakzioena berdin zero dira). Translaziozko mugimenduak egiten duen masa gorpuzki puntutzat hartzen da, eta v=wr du lastertasuna. Zilindroa ardatz finko baten inguruan ari da biraka. Beraz:

eta (a) ekuazioko elementuen ordez (b) ekuazioko elementuak jarriz gero, ekuazio hau ateratzen da:

2. Pendulu fisikoa
Gorputz gotor zurrun batek ardatz finko bati buruz duen momentuaren aplikazio praktiko bat pendulu fisikoa edo pendulu elkartua da.
Pendulu fisikoa esaten zaio grabitatearen eraginez ardatz finko horizontal baten inguruan marruskadurarik
gabe bira dezakeen edozein gorputz gotor zurruni (7.13 irudia). Gorputz horrek bere oreka posiziotik aldentzean
eratzen duen angelua 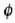 da,
eta
da,
eta  O edo suspentsio zentroaren
eta G edo gorputz horren masa zentroaren arteko distantzia. Hauek dira gorputz gotor horretan eragina duten
kanpoko indar bakarrak: G-n aplikatutako mg pisua, eta suspentsio ardatzak R-n duen erreakzioa.
O edo suspentsio zentroaren
eta G edo gorputz horren masa zentroaren arteko distantzia. Hauek dira gorputz gotor horretan eragina duten
kanpoko indar bakarrak: G-n aplikatutako mg pisua, eta suspentsio ardatzak R-n duen erreakzioa.
 ardatza hartuko da errotazio ardatztzat.
Orduan, gorputz horri eragiten dion mugimenduaren
ardatza hartuko da errotazio ardatztzat.
Orduan, gorputz horri eragiten dion mugimenduaren  osagaia
osagaia  da. Beraz, (7.27)
ekuazioaren arabera, ekuazio hau ateratzen da:
da. Beraz, (7.27)
ekuazioaren arabera, ekuazio hau ateratzen da:
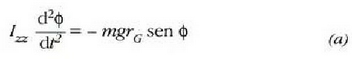
ekuazio horretan  penduluak z ardatzari
buruz duen inertzia momentua adierazten du. Aurreko ekuazio hori era honetara ere adieraz daiteke:
penduluak z ardatzari
buruz duen inertzia momentua adierazten du. Aurreko ekuazio hori era honetara ere adieraz daiteke:

Baina lekualdatzeak txikiak direnean,
orduan  , eta aurrekoekuaziotik
beste ekuazio hau ateratzen da:
, eta aurrekoekuaziotik
beste ekuazio hau ateratzen da:

Ekuazio horrek mugimendu armoniko soil bat adierazten du (ikus (2.69) ekuazioa). Eta beste ekuazio honek ekuazio horren angelu maiztasuna eta periodoa adierazten ditu:

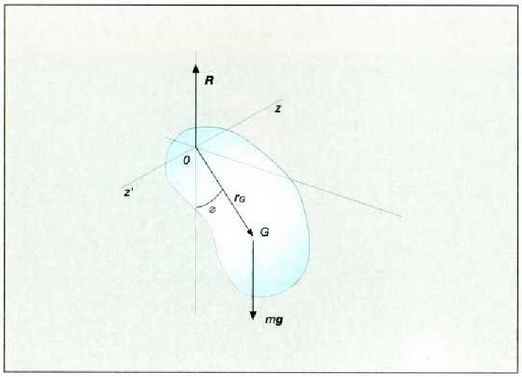
7.13: Pendulu Pikoa esaten zaio grabitatearen eraginez ardatz finko horizontal baten inguruan biraka ari den edozein gorputz zurruni.
Bada kasu berezi bat; gorputz horren masa guztia G puntuan kontzentratuta baldin badago eta gorputz
horren gainontzeko guztiaren ordez kontuan ez hartzeko moduko masa hari bat jartzen bada, luzera l duena,
orduan 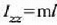 , eta beraz:
, eta beraz:
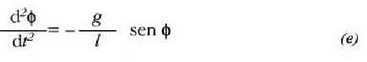
Hauek dira aurreko ekuazio horretan adierazita dagoen mugimenduaren maiztasuna eta periodoa:
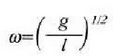 eta
eta

Pendulu horri pendu soila esaten zaio.
Inertzia momentuak
Inertzia momentuaren definizioa
Gorputz gotor zurrunen dinamikaren problema gehienetan inertzia momentuak agertzen dira; inertzia momentu horiek gorputz gotor zurrunak ardatz finko baten inguruan egiten duen errotazioan ere agertu ziren. Masek translaziozko mugimenduan duten zeregin beretsua dute inertzia momentuek errotaziozko mugimenduan.
Definizioz, gorputz gotor baten inertzia momentua 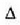 ardatzari buruz (7.14 irudia) ekuazio honen bidez adierazten da:
ardatzari buruz (7.14 irudia) ekuazio honen bidez adierazten da:

gorputz baten elementu bakoitzaren masa, dm, (halakotzat masa banaketa jarraitu bat harturik) eta masa horrek ardatzera duen d distantzia biderkatuz ateratzen diren terminoen batuketa adierazten du ekuazio horrek.
Definizio horren arabera, zero baino handiagoa den zenbaki positibo
baten bidez adierazten da beti inertzia momentua, zernahi ere den gorputz horren forma,
zeinahi ere den gorputz horren masa banaketa, edo zeinahi ere den errotazio ardatzaren posizioa.
CGS sisteman  du banakoa,
eta SI sisteman, berriz,
du banakoa,
eta SI sisteman, berriz, 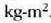 .
.
 denez (ikus (3.52) ekuazioa),
inertzia momentuak bolumenezko integralen bidez adieraz daitezke. Gorputz hori homogeneoa baldin bada gainera,
orduan badago p zeinua integraletik ateratzea.
denez (ikus (3.52) ekuazioa),
inertzia momentuak bolumenezko integralen bidez adieraz daitezke. Gorputz hori homogeneoa baldin bada gainera,
orduan badago p zeinua integraletik ateratzea.

Biratze erradioa
m-k gorputzaren masa osoa adierazten baldin badu, eta k honela definitzen den zenbaki positiboa baldin bada:

orduan zenbaki horri gorputzak  lerro zuzenari buruz duen biratze errradioa esaten zaio. Sistema zatiki bakar batez osatua dagoenean,
edozein lerro zuzenari buruzko biratze erradioa lerro zuzen horretara dagoen distantzia izango da, besterik gabe.
lerro zuzenari buruz duen biratze errradioa esaten zaio. Sistema zatiki bakar batez osatua dagoenean,
edozein lerro zuzenari buruzko biratze erradioa lerro zuzen horretara dagoen distantzia izango da, besterik gabe.
Gorputz hori koordenatu lauki zuzeneko sistema bati baldin badagokio (7.15 irudia), gorputz horrek x ardatzari buruz duen inertzia momentua ekuazio honen bidez definitzen da:

Ekuazio horren bidez jakin daiteke y, z, ardatzei buruzko inertzia momentuak zeintzuk diren, x, y, z letrak zirkuluan permutatuz. Beraz:

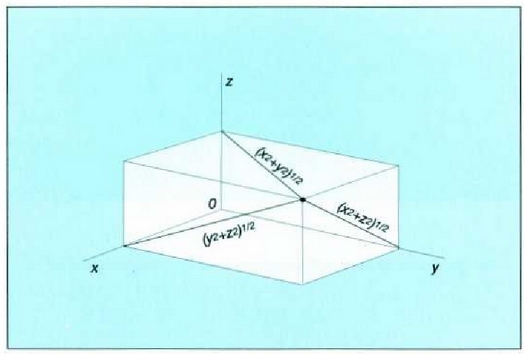
7.15: Koordenatu lauki zuzeneko sistema bati dagokion gorputz baten inertzia momentua
Inertzia momentua bi ardatz paralelori buruz. (Steiner-en teorema)
Gorputz jakin batean infinituak dira inertzia momentuak, nahi bezala aukeratutako
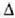 ardatzak zeinek bere
inertzia momentua du eta. Orain definituko da nola aldatzen den gorputz gotor zurrun baten inertzia momentua ardatz
horren beraren paralelo mugitzen den ardatz bati buruz, eta horretarako, aski da ardatzetako bat masen
zentrotik igarotzen den kasua kontuan hartzea.
ardatzak zeinek bere
inertzia momentua du eta. Orain definituko da nola aldatzen den gorputz gotor zurrun baten inertzia momentua ardatz
horren beraren paralelo mugitzen den ardatz bati buruz, eta horretarako, aski da ardatzetako bat masen
zentrotik igarotzen den kasua kontuan hartzea.
 baldin bada gorputz batek O
puntuari buruz duen masen zentroaren posizio bektorea, eta r' baldin bada masaren neurria
dm duen gorputz gotorraren gorpuzki puntu batek G puntuari buruz
duen posizio bektorea (7.16 irudia). Orduan:
baldin bada gorputz batek O
puntuari buruz duen masen zentroaren posizio bektorea, eta r' baldin bada masaren neurria
dm duen gorputz gotorraren gorpuzki puntu batek G puntuari buruz
duen posizio bektorea (7.16 irudia). Orduan:

(7.28) ekuazioaren arabera, ekuazio hau ateratzen da:

ekuazio horretan e banako bektore bat da, 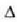 ardatzaren norabide eta noranzko bera duena. (7.34) ekuazioan r-ren ordez (7.33) ekuazioa jarriz geroz,
ekuazio hau ateratzen da:
ardatzaren norabide eta noranzko bera duena. (7.34) ekuazioan r-ren ordez (7.33) ekuazioa jarriz geroz,
ekuazio hau ateratzen da:
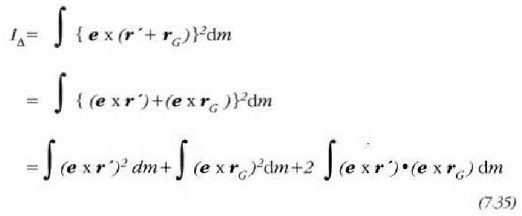
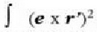 terminoak
terminoak
 inertzia momentua
adierazten du e-ren p raleloa den eta masen zentrotik igarotzen den ardatz bati buruz;
inertzia momentua
adierazten du e-ren p raleloa den eta masen zentrotik igarotzen den ardatz bati buruz;
 terminoak hau balio du:
terminoak hau balio du:

ekuazio horretan O-k eta G-k sortzen dituzten bi ardatz paraleloen distantzia adierazten du
 , eta gorputz horren
masa osoa m-k. Azkenik:
, eta gorputz horren
masa osoa m-k. Azkenik:
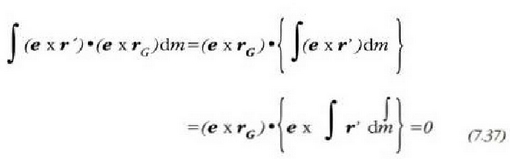
zeren eta, masen zentroaren definizioaren arabera, r' dm=0 baita. Honela idatz daiteke beraz:

alegia: Gorputz batek edozein ardatzi buruz duen inertzia momentua zein den jakiteko, gorputz horrek masen zentrotik igaroko den ardatz paralelo bati buruz duen inertzia momentuari gorputz horrek ardatz jakin horri buruz duen inertzia momentua gehitu behar zaio, jakintzat emanik masen zentroan daukala kontzentratua masa. Inertzia momentuen kalkulua asko errazten duen teorema horri Steiner-en teorema esaten zaio (edo "ardatz paraleloen teorema").
(7.38) ekuazioak beste gauza hau ere erakusten du: lerro zuzen jakin baten ardatz paralelo guztien artean, masen zentrotik igarotzen den horrek du inertzia momentu txikiena.
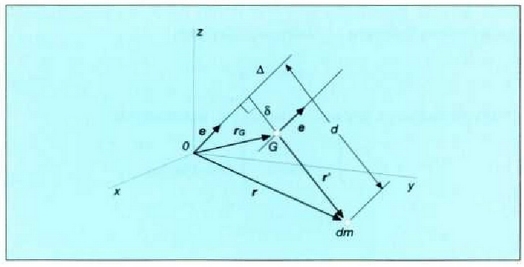
716 Gorputz batek ardatz jakin bati buruz duen inertzia momentua zein den jakiteko, gorputz osoaren masa ardatzen arteko distantziaren berreduraz biderkatuz gero, biderkatze horretan ateratzen den emaitza gehitu behar zaio lehenengo ardatzari buruz paraleloa den eta gorputz horren masen zentrotik igarotzen den ardatzaren inertzia momentuari.
Ardatz elkarzuten teorema
Ardatz perpendikularren teorema xafla lau eta mehen inertzia momentuak kalkulatzeko erabiltzen da.
Demagun Oxyz koordenatu lauki zuzeneko sistema bat dela, eta demagun orobat xaflaz=O planoan dagoela (7.17 irudia).
Baldin eta 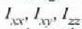 -k inertzia momentuak a
dierazten badituzte koordenatu ardatzei buruz, orduan
-k inertzia momentuak a
dierazten badituzte koordenatu ardatzei buruz, orduan

Eta, bistan denez,

alegia, xafla lau batek xafla horren beraren planoan dauden bi ardatz elkarzutei buruz duen inertzia momentuak batuz gero, xafla horrek berak berari buruz elkarzuta den eta ardatzen elkarguneetatik igarotzen den ardatzari buruz duen inertzia momentua ematen du.
Ardatz paraleloen teorema edozein gorputzi dagokio; ardatz elkarzuten teorema, berriz, xaflan bakarrik betetzen da.
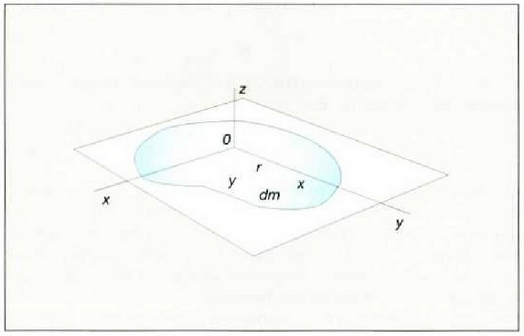
717: Xafla lau batek z ardatzari buruz duen inertzia momentua zein den jakiteko, xafla horrek berak x eta y ardatzei buruz dituen inertzia momentuak batu behar dira.
Adibidea.
Gorputz soil batzuen inertzia momentuak
Inertzia momentuak integralen bidez zehazten dira.
Orain ikusiko diren adibideetan gorputz bakoitza homogeneotzat hartuko da.
Eraztuna. Demagun masa m duen eta erradioa R duen eraztun bat (7.18 irudia). Eraztun horren planori buruz normala den eta eraztunaren erditik igarortzen denz ardatzari buruz duen inertzia momentua ekuazio honek definitzen du:

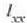 eta
eta
 momentuak berdinak direnez,
ardatz elkarzuten teorema aplikatuz gero, ekuazio hau ateratzen da:
momentuak berdinak direnez,
ardatz elkarzuten teorema aplikatuz gero, ekuazio hau ateratzen da:
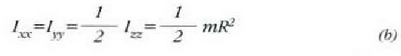

Eraztunaren ukitzaile den D ardatz bati buruzko inertzia momentua hau da, ardatz elkarzuten teoremaren arabera:

Disko zirkularra. Erradioa R cluen disko zirkular batek diskoari buruz elkarzuta den eta disko horren erditik igarotzen den z ardatzari buruz duen inertzia momentua zein den jakiteko, disko hori eraztun zirkularretan deskonposatu behar da (7.19 irudia).
Masa elemetu gisa erradioa r duen eta loditasuna dr duen eraztun bat hartuz gero,
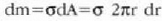 izando da,
izando da,
 izango da, 6 izanik azaleko dentsitatea.
Beraz, (a) ekuazioa aplikatuz, beste ekuazio hau ateratzen da:
izango da, 6 izanik azaleko dentsitatea.
Beraz, (a) ekuazioa aplikatuz, beste ekuazio hau ateratzen da:
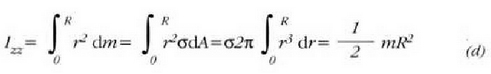

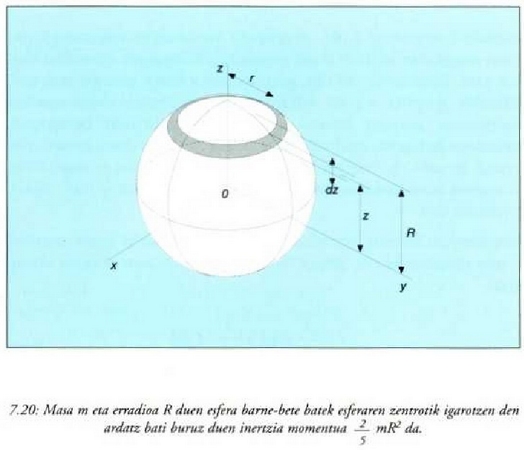
Esfera barne-betea. Aurreko ekuazio horri
esker jakin daiteke zein den esfera barne-bete baten inertzia momentua bere erdigunetik igarotzen den
 ardatz bati buruz.
DemagunR dela esfera horren erradioa, eta r dela 7.20 irudian agertzen den diskoaren erradioa.
ardatz bati buruz.
DemagunR dela esfera horren erradioa, eta r dela 7.20 irudian agertzen den diskoaren erradioa.
 denez, bere masak
denez, bere masak
 . balio du. Beraz, (d) ekuazioaren arabera,
. balio du. Beraz, (d) ekuazioaren arabera,
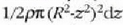 izango da disko horren inertzia momentua
izango da disko horren inertzia momentua
 ardatzari buruz, eta esfera horren inertzia
momentuak balio hau izango du:
ardatzari buruz, eta esfera horren inertzia
momentuak balio hau izango du:
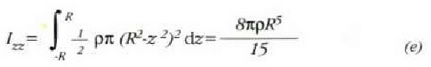
Baina, esfera horren masa  denez,
honela idatz daiteke ekuazio hori:
denez,
honela idatz daiteke ekuazio hori:

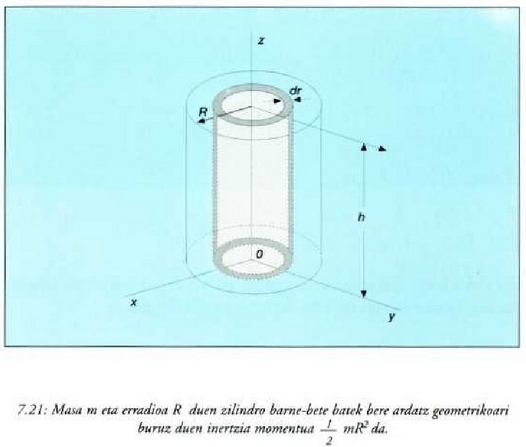
Zilindro barne-betea. Demagun erradioa R eta garaiera h duen zilindro barne-bete bat (7.21 irudia). Zilindro horrek bere ardatz geometrikoari buruz duen inertzia momentua kalkulatzeko, lehenik erradioa r eta lodiera dr duen eta irudian adierazita dagoen zilindroaren inertzia momentua dago definitu beharra. Zilindro mehe horren masa hau da:

ekuazio horretan p-k zilindroaren dentsitatea adierazten du. Eta z ardatzari buruz duen inertzia momentuak hau balio du:

Beraz:
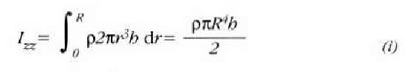
eta zilindroaren masa
 denez, ekuazio hau ateratzen da:
denez, ekuazio hau ateratzen da:

Gorputz gotor zurrun baten mugimendu laua
Mugimendu laua esaten zaio gorputz gotor zurrun baten mugimenduari, gorputz horren zatiki bakoitza plano bati buruz paraleloan lekualdatzen denean; adibidez, ibilbide zuzen batean zehar biraka dabilen diskoa. Mugimendu laua translazio baten eta errotazio baten ondoriotzat har daiteke. Translazio mugimendua definitzeko, ekuazio hau erabiltzen da:

ekuazio horretan m-k gorputzaren masa osoa adierazten du,
 masen zentruaren azelerazioa, eta F-k horra bildu diren indar sistemaren (kanpokoak eta erreakzioak) ondorioa.
Errotazio mugimendua definitzeko, ekuazio hau erabiltzen da:
masen zentruaren azelerazioa, eta F-k horra bildu diren indar sistemaren (kanpokoak eta erreakzioak) ondorioa.
Errotazio mugimendua definitzeko, ekuazio hau erabiltzen da:

ekuazio horretan  kanpoko indar guztiek masen zentroari buruz duten momentua da, eta
kanpoko indar guztiek masen zentroari buruz duten momentua da, eta
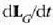 , berriz,
angelu momentuak masen zentroari buruz duen deribatua denborari buruz.
, berriz,
angelu momentuak masen zentroari buruz duen deribatua denborari buruz.
Adibidea. Masa m eta erradioa r duen zilindro bat malda
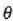 duen plano etzan batean behera itzulikatzen da.
Asmatu zilindro horren masen zentroaren azelerazioa.
duen plano etzan batean behera itzulikatzen da.
Asmatu zilindro horren masen zentroaren azelerazioa.
Ebazpena. Indar hauek dute eragina zilindro horretan: zilindroaren pisuak berak, mg, G masen zentroan duelarik eragina; eta planoaren R erreakzioak eta Fr (marruskadura indarra) planoan gorantz duelarik eragina baldin eta zilindroa beherantz itzulikatzen bada (7.22 irudia). Zilindroa itzulikatzen denean, G masen zentroa lekualdatu egiten da, eta zilindroa eratzen duten zatikiek G-ren inguruan biratzen dute. Horren ondorioz sortzen den mugimendua, beraz, translazio bat eta errotazio bat da.

7.22
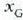 baldin bada masen zentroen planoari buruz paraleloa den lekualdatzea, hauxe izango du lekualdatze horrek ekuazioa:
baldin bada masen zentroen planoari buruz paraleloa den lekualdatzea, hauxe izango du lekualdatze horrek ekuazioa:

Fr -ri baizik ez dagokio G masen zentroari buruzko momentua. Beraz:

ekuazio horretan 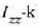 zilindro horrek ardatzari buruz duen inertzia momentua adierazten du, eta a-k ardatz horri
buruzko angelu azelerazioa adierazten du.
zilindro horrek ardatzari buruz duen inertzia momentua adierazten du, eta a-k ardatz horri
buruzko angelu azelerazioa adierazten du.
Soil-soilik zinematikoa den erlazioa hau da:

(a) (b) eta (c) ekuazioetatik beste ekuazio hau ateratzen da:
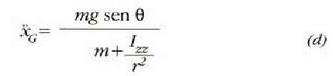
eta  dela kontuan harturik,
ekuazio hau aterako da azkenik:
dela kontuan harturik,
ekuazio hau aterako da azkenik:

Gorputz gotor zurrun batek ardatz finko baten inguruan duen errotaziozko energia zinetikoa
Gorputz gotor zurrun baten energia zinetikoa esaten zaio, definizioz, magnitude eskalar honi:

ekuazio horretan v-k posizioa r duen dm masa puntu baten lastertasuna adierazten du.
Gorputz horrek z ardatz finko baten inguruan biratzen baldin badu, orduan
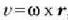 , eta (7.43) ekuazioan
berdintza hori jartzen bada v-ren ordez, ekuazio hau ateratzen da:
, eta (7.43) ekuazioan
berdintza hori jartzen bada v-ren ordez, ekuazio hau ateratzen da:

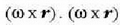 biderkadura mistoan.
eta x truka daitezkeenez, hau ateratzen da:
biderkadura mistoan.
eta x truka daitezkeenez, hau ateratzen da:
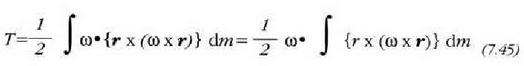
eta aurreko ekuazioan bezalaxe, integral horrek
 gorputzaren angelu
momentua adierazten duenez, hau aterako da:
gorputzaren angelu
momentua adierazten duenez, hau aterako da:
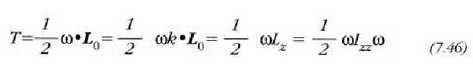
Beraz,

ekuazio horretan  -ri gorputz
zurrunak w ardatzaren inguruan mugitzean sortzen duen errotaziozko energia zinetikoa esaten zaio.
Errotazioan ari den gorputz gotor baten energia zein den jakiteko, gorputz horrek errotazio ardatzari
buruz duen inertzia momentua gorputz horren angelu lastertasunaren berreduraz biderkatu behar da,
eta biderkatze horrek sortzen duen emaitzaren erdiak ematen du energia hori. Gainera, T-ren balioa
ez dago errotazioaren noranzkoaren mende.
-ri gorputz
zurrunak w ardatzaren inguruan mugitzean sortzen duen errotaziozko energia zinetikoa esaten zaio.
Errotazioan ari den gorputz gotor baten energia zein den jakiteko, gorputz horrek errotazio ardatzari
buruz duen inertzia momentua gorputz horren angelu lastertasunaren berreduraz biderkatu behar da,
eta biderkatze horrek sortzen duen emaitzaren erdiak ematen du energia hori. Gainera, T-ren balioa
ez dago errotazioaren noranzkoaren mende.  -ko
banakoak
-ko
banakoak 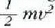 -koen berdinak dira.
-koen berdinak dira.
Mugimendu lauean, translazio batek eta errotazio batek eratzen duten mugimenduan, alegia, hauxe da gorputzaren energia zinetikoa:

ekuazio horretan  gorputz gotorrak masen zentrotik mugimenduaren planora doan normalari buruz duen inertzia
momentua adierazten du, eta
gorputz gotorrak masen zentrotik mugimenduaren planora doan normalari buruz duen inertzia
momentua adierazten du, eta  ,
berriz, masen zentroen lastertasuna. Ekuazio honek
,
berriz, masen zentroen lastertasuna. Ekuazio honek

G-ren inguruko errotazio mugimendutik independentea izanik, gorputz horren translaziozko energia zinetikoa adierazten du, eta beste ekuazio honek

translazio mugimendutik independentea izanik, G-ren inguruko errotaziozko energia zinetikoa ematen du. Beraz, gorputzaren energia osoa translaziozko eta errotaziozko energia zinetikoez dago eratuta; alegia,

Adibidea. Masa m duen eta gainalde horizontal batean marruskadurarik gabe itzulikatzen
den disko baten energia zinetikoa asmatu, disko horren masen zentroaren lastertasuna
 dela jakinik.
dela jakinik.
Ebazpena. Zilindro horrek mugimendu lau bat egiten du (7.23) irudia. (7.48) ekuazioaren arabera, ekuazio hau ateratzen da:
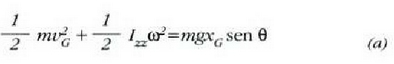
 denez,
non R zilindroaren erradioa baita, eta
denez,
non R zilindroaren erradioa baita, eta 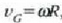 ,
aurreko ekuazioan elementu hauek jarriz besteen ordez beste
ekuazio hau ateratzen da:
,
aurreko ekuazioan elementu hauek jarriz besteen ordez beste
ekuazio hau ateratzen da:
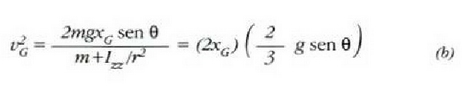
Energia zinetiko osoaren 2/3 translaziozkoa da, eta 1/3, berriz, errotaziozkoa.

7.23
Energiaren ekuazioa
(7.27) ekuazioko bi osagaiak eta 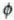 biderkatzen badira, ekuazio hau ateratzen da:
biderkatzen badira, ekuazio hau ateratzen da:

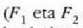 erreakzioek ez dute lanik egiten,
aplikazio puntuak finkoak dituzte eta). Gorputz gotorrean eragina duten kanpoko indarrak kontserbadoreak
baldin badira, orduan, energia potentzialari
V deiturik, eta energiaren kontserbazioaren printzipioaren arabera,
hau ateratzen da:
erreakzioek ez dute lanik egiten,
aplikazio puntuak finkoak dituzte eta). Gorputz gotorrean eragina duten kanpoko indarrak kontserbadoreak
baldin badira, orduan, energia potentzialari
V deiturik, eta energiaren kontserbazioaren printzipioaren arabera,
hau ateratzen da:

eta (7.52) ekuazioa kontuan harturik:

Aldagaiak bereiziz eta integrazioa eginez, ekuazio hau ateratzen da:
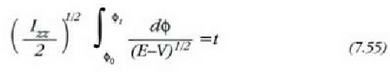
ekuazio horri esker  atera daiteke t-ren arabera,
baldin eta V energia potentziala eta E konstantea ezagutzen badira.
atera daiteke t-ren arabera,
baldin eta V energia potentziala eta E konstantea ezagutzen badira.
Adibidea. 7.12 ataleko adibidea ebatzi, energiaren kontserbazio printzipioa aplikatuz.
Ebazpena. Energiaren kontserbazio printzipioak adierazten duenez, itzulika ari den
zilindroaren energia potentzialaren galera eta energia zinetikoaren irabazia berdinak dira.
Kasu honetan, masen zentroaren translaziozko energia zinetikoak eta masen zentroaren inguruan
errotazioan dagoen energia zinetikoak eratzen dute energia zinetikoa. Demagun, errazago ulertzeko,
zilindroa geldirik zegoela hasieran eta 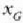 distantzia itzulikatzen duela (7.24 irudia). Energiaren ekuazioari esker ekuazio hau adieraz daiteke:
distantzia itzulikatzen duela (7.24 irudia). Energiaren ekuazioari esker ekuazio hau adieraz daiteke:
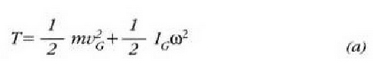
 -ren eta
-ren eta
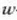 -ren artean
-ren artean
 erlazioa dagoenez, orduan:
erlazioa dagoenez, orduan:
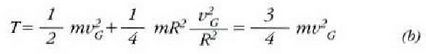
Zilindro horren lastertasunak ez du zerikusirik zilindroaren masarekin edo dimentsioekin. (b) ekuazioaren ondorioz esan daiteke masen zentroaren azelerazio konstanteak hau balio duela:


7.24
8. Gorputz zurrunen estatika
Grabitate zentroa
Grabitate indarra gorputz zurrunen mugimenduak duen indarretako bat da. Ez da berez indar bat, indar askoren ondorioa baizik.
Gorputzaren zatiki bakoitzak grabitazio indar baten eragina izaten du.
Demagun M masa duen gorputz bat zatiki kopuru handi batean dagoela zatitua, eta n duela izena zatiki
kopuru horrek; Lurrak masa m duen i zatikian daukan grabitazio indarra
 da. Indar horrek beherantz du norabidea,
Lurrerantz. g grabitateak lurralde oso batean azelerazio berbera sorrarazten badu, lurralde horretan
grabitazio eremu uniforme bat dagoela esaten da orduan; alegia, g-k magnitude,
norabide eta noranzko bera du lurralde horretako leku guztietan.
Gorputz zurrun bat grabitate eremu uniforme batean dagoenean, gorputz horretako
zatiki bakoitzak grabitate bera du, eta zatiki horien pisuak indar elkarri buruz paraleloak dira.
Demagun Lurraren grabitazio eremua uniformea dela; badago frogatzea gorputz batean eragina duten
pisu banako guztien ordez Mg jar daitekeela, gorputz horren masaren zentroan beherantz egiten duen
indar bakarra hain zuzen.
da. Indar horrek beherantz du norabidea,
Lurrerantz. g grabitateak lurralde oso batean azelerazio berbera sorrarazten badu, lurralde horretan
grabitazio eremu uniforme bat dagoela esaten da orduan; alegia, g-k magnitude,
norabide eta noranzko bera du lurralde horretako leku guztietan.
Gorputz zurrun bat grabitate eremu uniforme batean dagoenean, gorputz horretako
zatiki bakoitzak grabitate bera du, eta zatiki horien pisuak indar elkarri buruz paraleloak dira.
Demagun Lurraren grabitazio eremua uniformea dela; badago frogatzea gorputz batean eragina duten
pisu banako guztien ordez Mg jar daitekeela, gorputz horren masaren zentroan beherantz egiten duen
indar bakarra hain zuzen.
Demagun gorputz baten masa zentrotik igarotzen den ardatz bat,
eta aukera dezagun C masa zentroa koordenatuen sorburutzat. Hau da orduan
 ardatzarekiko unea -ardatz horiC-tik
igarotzen da eta normala da irudiari buruz-, gorputzaren masa zatiki bakoitzean eragina duten pisu indar bertikalen
ondorioz (14.2 irudia):
ardatzarekiko unea -ardatz horiC-tik
igarotzen da eta normala da irudiari buruz-, gorputzaren masa zatiki bakoitzean eragina duten pisu indar bertikalen
ondorioz (14.2 irudia):

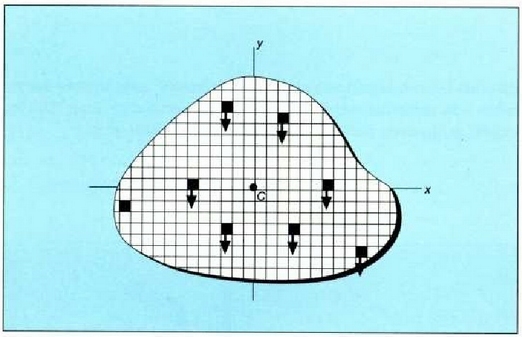
8.2: Grabitazio eremu uniforme batek gorputz bat eratzen duten oinarrizko masetan sortzen dituen indarrak
Ekuazio horretan  da mi masako i zatikiko x koordenatua.
Nolanahi ere,
da mi masako i zatikiko x koordenatua.
Nolanahi ere,  berdin zero da,
masa zentroaren definizioaren arabera, eta, beraz,
berdin zero da,
masa zentroaren definizioaren arabera, eta, beraz,  berdin zero. Modu berean froga daiteke masa zentrotik igarotzen diren x eta y ardatzei buruzko momentuek,
berdin zero. Modu berean froga daiteke masa zentrotik igarotzen diren x eta y ardatzei buruzko momentuek,
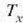 eta
eta
 , zero balio dutela.
, zero balio dutela.
Emaitza bera ateratzen da gorputza jarraitua baldin bada eta zatiki kopuru infinitoan zatitua
 baldin badago.
Kalkulu integralaren bidez ebazten da hori.
baldin badago.
Kalkulu integralaren bidez ebazten da hori.
 ardatzari buruz paraleloa den edozein ardatzi buruzko unea eta
beherantzako indar osoak,
ardatzari buruz paraleloa den edozein ardatzi buruzko unea eta
beherantzako indar osoak,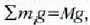 ,
masa zentroan aplikatuko balitz izango lukeen unea berdinak dira; eta gauza bera gertatzen zaio x edo y
ardatzaren beste edozein ardatz paralelori. Horren ondorioz, indar bakarra egon daiteke, Mg,
gorputzaren masako zatiki guztietan eragina duten grabitazio indarren ordez; indar hori
gorputz horren pisu osoaren berdina da eta masa zentroan du eragina. Balio bereko ondoriozko
grabitate indarrak eragina duen puntuari grabitate zentrua esaten zaio.
,
masa zentroan aplikatuko balitz izango lukeen unea berdinak dira; eta gauza bera gertatzen zaio x edo y
ardatzaren beste edozein ardatz paralelori. Horren ondorioz, indar bakarra egon daiteke, Mg,
gorputzaren masako zatiki guztietan eragina duten grabitazio indarren ordez; indar hori
gorputz horren pisu osoaren berdina da eta masa zentroan du eragina. Balio bereko ondoriozko
grabitate indarrak eragina duen puntuari grabitate zentrua esaten zaio.
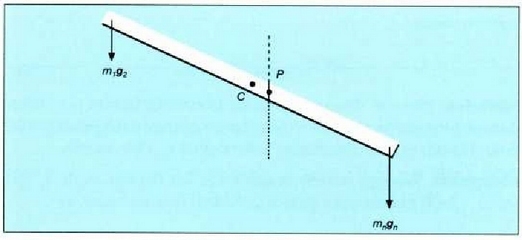
8.3: C masa zentroa eta Pgrabitate zentroa ez datoz bat, Lurraren grabitazio eremua ez baita uniformea
Grabitate zentroa eta masa zentroa bat etortzea Lurraren grabitazio eremua uniformea zela uste izateak ekarri zuen.
Izan ere, uste hori ez da guztiz zuzena, g-ren magnitudea aldatu egiten baita Lurraren zentrora dagoen distantziaren
arabera, eta, gainera, g-ren norabidea erradiala baita edozein puntutik Lurraren zentroratz. Gertaera horrek zer
ondorio duen ikusteko, demagun barra uniforme bat kilometro asko luze dena, eta makurtua bertikalari buruz
Lurraren grabitazio eremuan, 14.3 irudian ikusten den bezala. Gorputz baten grabitate zentroa balio bereko
ondoriozko grabitate indarraren eragina duen puntu horixe da. Puntu hori eta gorputz horretan, eta orekan jartzeko,
kontrako noranzkoan dagoen indar bakarra aplikatuko den puntua berdinak dira. Grabitazio eremua uniformea balitz,
Mg indar bakarra masaren zentroan aplikatzeak translaziozko eta errotaziozko orekan jarriko luke barra.
Baina eremu hori ez da uniformea, eta  -n
duen balioa
-n
duen balioa  -n duen balioa baino txikiagoa da.
Beraz, masa zentrotik beheraxeago P distantzia jakin batera dagoen P puntua da gorputz hori orekan jartzeko indar bakarra
eragin behar den puntua. Gainera, gorputz horren orientazioa aldatuz gero, orobat aldatu behar da gorputz hori orekan
jartzeko indarra eragin behar zaion P puntuaren posizioa. Beraz, kasu horretan grabitate zentroak ez du garrantzi handirik.
Ez dator bat masaren zentroarekin, eta gehiago: gorputz horrekiko posizioa ere aldatzen du gorputz hori mugitzen denean.
-n duen balioa baino txikiagoa da.
Beraz, masa zentrotik beheraxeago P distantzia jakin batera dagoen P puntua da gorputz hori orekan jartzeko indar bakarra
eragin behar den puntua. Gainera, gorputz horren orientazioa aldatuz gero, orobat aldatu behar da gorputz hori orekan
jartzeko indarra eragin behar zaion P puntuaren posizioa. Beraz, kasu horretan grabitate zentroak ez du garrantzi handirik.
Ez dator bat masaren zentroarekin, eta gehiago: gorputz horrekiko posizioa ere aldatzen du gorputz hori mugitzen denean.
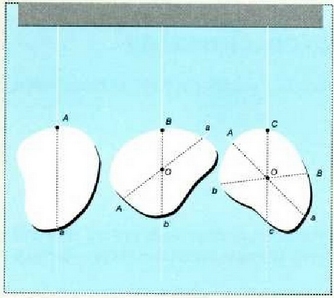
8.4: Masa zentroa zuzen-zuzenean O suspentsio puntuaren azpian dagoenez beti, O definitzeko aski da xafla bat bi puntu deberdinetatik zintzilikatzea.
Mekanikako ia problema guztietan aztertzen diren objektuak neurriz txikiak direnez, g nabarmen aldatzen den distantziekin konparatuz gero, uste izan daiteke g uniformea dela gorputz osoan. Masa zentroa eta grabitate zentroa puntu bera balira bezala har daitezke orduan. Izan ere, puntu bera izate hori esperimentu bidez forma irregularreko objektuen masa zentroa definitzeko erabil daiteke. Adibidez, xafla mehe formaz irregular baten masa zentroa non dagoen bilatuko da orain, 14-4 irudian agertzen den bezala. Gorputz horren beraren ertzeko edozein A puntutik soka batez zintzilikatu behar da gorputz hori. Gorputza geldi geratzen denean, grabitate zentroak berme puntuaren azpian zuzen-zuzenean egon behar du, Aa lerroko lekuren batean, horrela bakarrik baliogabetzen baita sokaren eta pisuaren ondoriozko unea. Gero, ertzeko B puntutik zintzilikatuko cla gorputz hori. Grabitate zentroak Bb-ko lekuren batean egon behar du berriz ere. Aa eta Bb lerro zuzenen arteko puntu komun bakarra O da, elkargunea, eta beraz puntu horrek izan behar du grabitate zentroa. Ertzeko beste edozein puntutik zintzilikatzen bada gorputz hori, C-tik adibidez, Cc lerro bertikala O puntutik igaroko da. Eremu hori uniformetzat jo denez, grabitate zentroa eta masa zentroa puntu berean daude, eta puntu hori, beraz, O puntuan dago.
Oreka estatikoaren adibideak
Oreka estatikoaren baldintzak aplikatzerakoan (ondoriozko indarra zero, eta ondoriozko momentua edozein ardatzi buruz zero), era askotara argitu eta erraztu daiteke prozedura hori.
Lehenik irudizko limite bat marraztuko da sistema jakin baten inguruan. Horrela ziur jakingo da zer gorputzetan edo gorputz sistematan aplikatuko (liren oreka estatikoaren legeak. Prozesu horri sistema bakartzea esaten zaio.
Bigarrenik, kanpoko indar guztien magnitudea, norabidea, noranzkoa eta aplikazio puntua adieraziko duten bektoreak marraztu behar dira. Hasieran marraztu den limiteaz kanpotik eragiten duen indarra da kanpoko indarra. Estatikan kanpoko indarren adibide asko daude: grabitazio indarrak eta limitea zeharkatzen duten sokek, alanbreek, ziriek eta hagek eragiten dituzten indarrak. Indarren batek zer noranzko duen jakin behar izaten da maiz. Horretarako, indar eragilean zehar irudizko ebaki bat egin behar da indar eragile horrek limitea gurutzatzen duen puntuan. Ebaki horren muturrek elkarrengandik bereizteko joera baldin badute, indarrak kanpo aldera egiten du. Zalantzarik sortuz gero, noranzkoa nahi bezala aukeratu behar da. Problema hori ebazterakoan balioa negatiboa baldin bada, horrek esan nahi du indar horren noranzkoa uste izan denaren kontrakoa dela. Sistema horretan eragina duten kanpoko indarrak baizik ez dira hartu behar kontuan; barruko indar guztiek binaka elkar baliogabetzen dute.
Hirugarrenik, orekaren lehenengo baldintza aplikatu aurretik koordenatu ardatz egokiak aukeratu behar dira kanpoko indarrak deskonposatzeko. Kalkuluak errazteko egiten da hori. Koordenatu egokiei berehala antz eman ohi zaie.
Laugarrenik, momentu ardatz egoki bat aukeratu behar da, kalkuluak errazteko. Bi indar ezezagunek edo gehiagok elkar ebakitzen duten puntuan hartzen den ardatzak automatikoki baliogabetzen ditu indar horien momentuak. Kanpoko indar guztien ondoriozko uneak zero izan behar du edozein ardatzi buruz, oreka egongo bada. Barruko momentuek binaka elkar baliogabetzen dute.
Adibidea (a) Altzairuzko barra uniforme bat, metro batekoa, balantza banatan dago bermatua muturretan (14-5 irudia). Barra horrek 4.0 nt pisatzen du. Balantzek zer neurri markatzen duten jakin behar da.
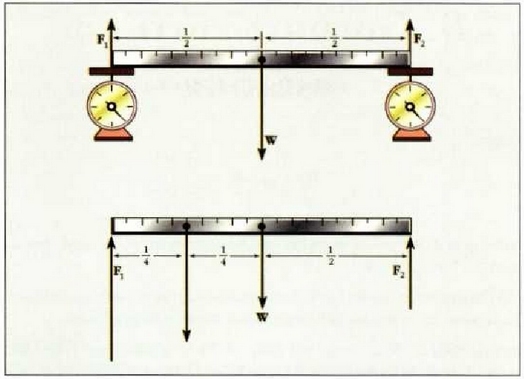
14.5: (a) la adibidea. Altzairuzko barra uniforme bat malgukizko balantza banatan dago bermatua. (b) I b adibidea. w pisua barra horren mutur batetik dagoen
Adibide honetan barra da sistema. Barran eragina duten indarrak W dira,
grabitate zentroan beherantz egiten duen grabitazio indarra
 indarrak
indarrak 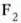 da,
eta balantzek muturretan barrari gorantz eragiten dizkioten indarrak F 2 dira.
Indar horiek 14-5a irudian ikusten dira. Newtonen hirugarren legearen arabera,
balantza batek barra horretan egiten duen indarra barrak balantzan egiten duenaren berdina eta kontrakoa da.
da,
eta balantzek muturretan barrari gorantz eragiten dizkioten indarrak F 2 dira.
Indar horiek 14-5a irudian ikusten dira. Newtonen hirugarren legearen arabera,
balantza batek barra horretan egiten duen indarra barrak balantzan egiten duenaren berdina eta kontrakoa da.
Beraz, balantzek zer markatzen duten jakiteko,
 eta
eta
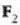 magnitudeak definitu behar dira.
magnitudeak definitu behar dira.
Translaziozko orekarako (Ec. 14-1) baldintza hau bete behar da:
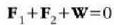
Indar guztien eragina bertikala da; beraz, y koordenatuen ardatz bertikala aukeratuz gero, ez da beste ardatzik aztertu beharrik. Orduan ekuazio eskalar hau ateratzen da:

Errotaziozko oreka zein den jakiteko, barrak edozein ardatzarekiko duen ondoriozko momentuak zero izan behar du. Errotazioa marrazkiaren planoari elkarzut den edozein ardatzaren ingurukoa izan daiteke. Aukera bedi grabitate zentrotik igarotzen den ardatz bat. Orduan, erlojuaren noranzkoa positibotzat harturik, eta kontrako noranzkoa, berriz, negatibotzat, hau da errotaziozko oreka betetzeko bete behar den baldintza (Ec. 14-3):

alegia,
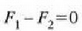
Bi ekuazio horiek konbinaturik, hau ateratzen da:

Balantza bakoitzak 2.Ont. markatzen du, uste izatekoa zen bezala.
Barraren mutur batetik igaroko zen ardatz bat aukeratuz gero, emaitza bera aterako litzateke. Adibidez, eskuineko muturretikigarotzen den ardatz bati buruzko momentuak hartuz gero, hau ateratzen da:

alegia,
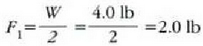
Balio hori 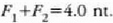 -rekin konbinatuz gero,
-rekin konbinatuz gero,
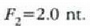 ateratzen da, lehen bezala.
ateratzen da, lehen bezala.
(b) Demagun 6.0 nt-ko bloke bat jartzen dela metro bateko barrako 25 zentimetro markan. Zer neurri ateratzen da balantzetan?
Barran eragina duten kanpoko indarrak 14-5b irudian ageri dira, eta w da blokeak barran egiten duen indarra. Orekaren lehenengo baldintza hau da:
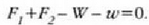
W=4.0 nt denean eta w=6.0 nt, hau ateratzen da:

Barraren ezkerreko muturretik igarotzen den ardatz bat hartuz gero, hau da orekaren bigarren baldintza:

W=4.0 nt denean eta w=6.0 t, hau ateratzen da:

Emaitza hori lehenengo ekuazioan jarriz gero, hau ateratzen da:
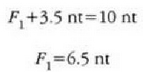
Ezkerreko balantzak 6.5 nt markatuko du, eta eskuinekoak, berriz, 3.5, orekan baitaude.
Problema honetan zergatik ez dira indarren bi baldintza baizik betetzen, eta ez indar guztiak plano berean daudenean sortzen diren problemetan betetzen diren hiru baldintzak?
14.6
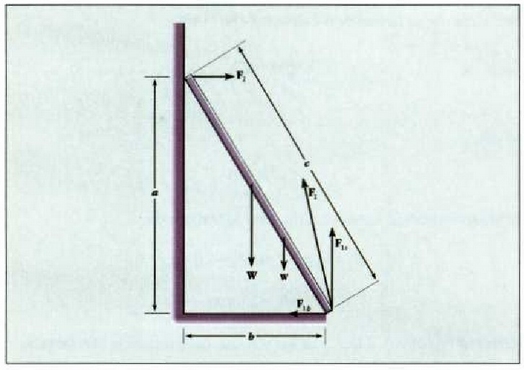
Adibidea. (a) 18.29 metro luze den eta 445 nt pisatzen duen eskailera batek pareta batean du bermea lurretik 14.63 metrotara dagoen puntu batean. Oinarritik hasi eta luzeraren heren batera du eskailera horrek grabitate zentroa. 712 nt pisatzen duen gizon bat eskaileraren erdialderaino igo da. Paretak marruskadurarik ez duela jakintzat emanik, eskailerak eta gizonak lurrean eta paretan egiten duten indarra zein den jakin behar da.
Eskaileran eragina duten indarrak 14-6 irudian agertzen dira.
Eskaileran dagoen gizonaren pisua W da, eta w, berriz, eskaileraren beraren pisua.
Lurrak  indarra egiten du eskaileran.
indarra egiten du eskaileran.
 , osagai bertikala da,
eta
, osagai bertikala da,
eta  indar horren osagai
horizontala (marruskaduraren eraginez). Paretak marruskadurarik ez duenez, bere gainaldeari buruz
normala den indarra baizik ez dezake egin,
indar horren osagai
horizontala (marruskaduraren eraginez). Paretak marruskadurarik ez duenez, bere gainaldeari buruz
normala den indarra baizik ez dezake egin,  Datu hauek ematen dira:
Datu hauek ematen dira:

Irudi horren geometriatik hau ateratzen da: b=10.97 m. W eragin lerroak paretatik b/2 distantziara ebakitzen du lurra, eta w eragin lerroak paretatik 2b/3 distantziara ebakitzen du lurra.
x-en ardatza lurrean aukeratzen da, etay-ren ardatza, berriz, paretan. Orduan, indar horiek baldintza hauek bete behar dituzte translaziozko oreka egon dadin (Ec. 14-2):

Errotaziozko orekarako, (Ec. 14-4) lurra ukitzen duen puntutik igaroko den ardatz bat aukeratu behar da, eta hau ateratzen da:
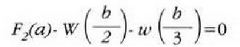
Zenbakizko datuak erabiliz, hau lortzen da:

Newtonen hirugarren legearen arabera, lurrak eta paretak eskaileran egiten dituzten indarrak eskailerak lurrean eta paretan egin dituztenaren berdinak eta kontrakoak dira. Beraz, paretan eragina duen indar normala 378.25 nt da, eta lurrean eragina duen indarrak 1 157 nt osagaia du beherantz eta 278.25 nt osagaia eskuinerantz.
(b) Lurraren eta eskaileraren arteko marruskadura estatikoaren koefizientea
 baldin bada,
zer alturataraino igo daiteke gizona eskailera irristatzen hasi baino lehen?
baldin bada,
zer alturataraino igo daiteke gizona eskailera irristatzen hasi baino lehen?
x baldin bada gizonak eskailera irristatzen hasi baino lehen igo dezakeen eskaileraren luzera osoaren zatia, orduan hauek dira oreka baldintzak:
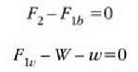
eta
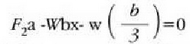
Zeinu bakoitzari bere balioa emanez gero, hau ateratzen da:
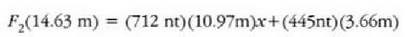

Beraz,

eta

Gehienezko marruskadura estatikoa honela definitzen da:

Beraz,

eta
x=0.658
beraz, gizon horrek metro hauek egin ditzake eskaileran gora:
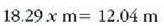
eskailera irristatzen hasi baino lehen.
Adibide honetan eskailera dimentsio bakarreko objektutzat hartu da, paretan eta lurrean ukitze puntu bana duena. Pentsatu beharra dago aldez aurreko baldintza horiek zenbatean mugatzen duten eskailerak mutur bakoitzean bi ukitze puntu dituen kasu ez beste hau bezain artifizialaren ebazpena.
Paretak marruskadurarik ez duela uste izateko arrazoia aurrerago aztertuko da. Zein ote da?
Adibidea. (a) Habe uniforme bat paretan giltzatua dago. Paretan finko dagoen alanbre bat habe horren beste muturrari dago lotua, giltzaduratik d distantziara. Alanbre hori horizontala da habearen muturrean soka finko batetik w pisua zintzilikatzen denean. Habeak W pisua baldin badu eta l luzera, alanbrearen tentsioa eta giltzadurak habean egiten dituen indarrak aurkitu behar dira.
14-7 irudian F habean eragina duten indar guztiak agertzen dira; giltzadurak habean
duen indarrak osagai horizontal eta bertikal bana ditu,
 eta
eta
 , hurrenez hurren.
T habeari tira egiten dion alanbre horizontalaren tentsioa da; w, habetik zintzilik dagoen
gorputzaren pisuak sokari eragiten dion tentsioa; eta W grabitate zentroan eragina duen habearen pisua da.
, hurrenez hurren.
T habeari tira egiten dion alanbre horizontalaren tentsioa da; w, habetik zintzilik dagoen
gorputzaren pisuak sokari eragiten dion tentsioa; eta W grabitate zentroan eragina duen habearen pisua da.
Ardatz horizontalak eta bertikalak hartuz gero, hau ateratzen da translaziozko oreka zein den jakiteko:
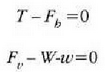
Giltzaduratik igarotzen den ardatz bat aukeratuz gero hau ateratzen da errotaziozko orekarako,

 eta
eta
 ezezagunak dira.
Beste kopuruei zenbakizko balio hauek emanez gero:
ezezagunak dira.
Beste kopuruei zenbakizko balio hauek emanez gero:

Orduan,
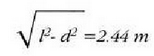
eta, balio horiek aurreko ekuazioan zeinuen ordez jarriz:

eta hortik hau ateratzen da:
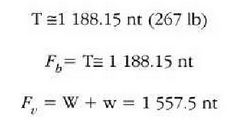
(b) Demagun zintzilik dagoen gorputz horren ordez 890 nt pisatzen duen beste gorputz bat jartzen dela, eta orduan habeak 30 ° ko angelu bat eratzen duela horizontalarekin batera (14-7b). Alanbreak duen tentsioa eta giltzadurak habean egiten dituen indarrak aurkitu behar dira.
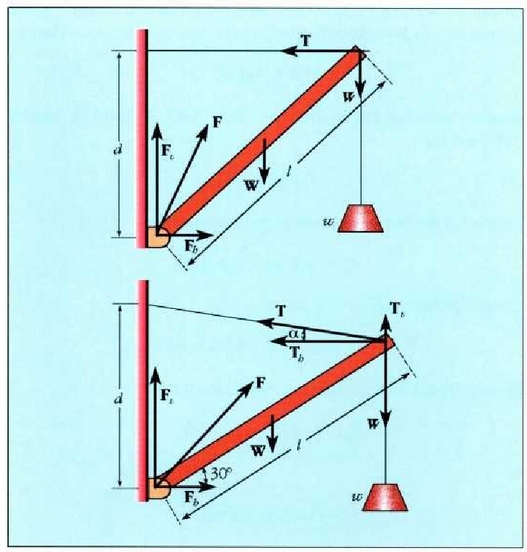
14.7 (a) 3a irudia. 3-4-5 triangelu bat eratzen duen kable horizontal batek habe giltzatu bati eusten dio. (b). 3b adibidea. Pisu bat eransten zaio, eta habeak eta horizontalak 30 °ko angelua eratzeko moduan luzatzen da alanbrea
Kasu horretan alanbrea ez da horizontal egongo. T-ren osagai bathorizontala izango da eta bestea bertikala,
 eta
eta
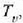 hurrenez hurren.
hurrenez hurren.
Translaziozko orekaren baldintzak hauek dira:
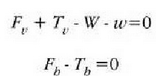
T-ren eta n-ren arteko elkargunetik igarotzen den ardatz bat aukeratuz gero, hau ateratzen da errotaziozko orekarako:

Datu hauek jakinez gero

Beraz,

eta

beraz,
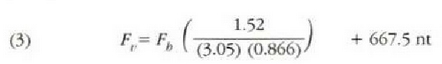
Orain lau ezezagun daude ekuazio horretan,
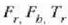 eta
eta
 eta, alegia.
Problema ebatzi ahal izateko, heste erlazio bat behar da kopuru horien artean.
eta, alegia.
Problema ebatzi ahal izateko, heste erlazio bat behar da kopuru horien artean.
 eta
eta
 batuketak T ondoriozko
bektorea eman behar du alanbrearen erlazioan. Alanbreak ezin du bere norabideari buruz
zeharkakoa den inclarrik eman edo eutsi. (Baina habeaz ezin cla horrelakorik esan). Beraz, hau da laugarren erlazioa:
batuketak T ondoriozko
bektorea eman behar du alanbrearen erlazioan. Alanbreak ezin du bere norabideari buruz
zeharkakoa den inclarrik eman edo eutsi. (Baina habeaz ezin cla horrelakorik esan). Beraz, hau da laugarren erlazioa:
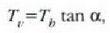
ekuazio horretan  , halako moduan non
, halako moduan non

(1) eta (4) konbinatuz, ekuazio hau ateratzen da:

(2) eta (3) konbinatuz, hau ateratzen da:

Ekuazio horiek batera ebatziz, hau ateratzen da:

eta

(2)tik hau ateratzen da

(1)etik hau ateratzen da
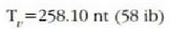
Alanbrearen tentsioa hau izango da orduan:

eta giltzadurak 2 247.25 nt (505 ib)ko indar horizontala egingo du, eta 1966.90 nt (442 ib)ko indar bertikala habean.
Aurreko adibideetan indar ezezagunen kopurua indarrak erlazionatzen dituen ekuazio independenteen kopurura mugatu da. Indar guztiek eragina plano batean dutenean, orekazko hiru ekuazio independente baizik ezin dira izan, bat errotaziozko orekarako planoari buruz normala den edozein ardatzi dagokionez, eta beste bi translazio orekarako planoan. Nolanahi ere, hiru indar ezezagun baino gehiago izaten dira askotan. Adibidez, 2-a adibideko eskaileraren probleman, ez bada marruskadurarik gabeko paretaren hipotesia hartzen, lau kopuru eskalar ezezagun ateratzen dira: paretak eskaileran egiten duen indarraren osagai horizontalak eta bertikalak eta lurrak eskaileran egiten duen indarraren osagai horizontala eta bertikala. Hiru ekuazio eskalar besterik ez daudenez, indar horiek ezin dira zehatz definitu. Indar ezezagun horietako bati edozein balio emanez definitu ahal izango dira beste hiru indarrak. Indar ezezagun horietako bati balio jakin bat emateko zertan oinarriturik ez izanez gero, infinitua izango da matematikaren bidez eman daitezkeen ebazpen posibleen kopurua. Beraz, problema horri ebazpen bakarra emateko, beste erlazio independente bat aurkitu beharra dago indar ezezagun horien artean.
Autoa da definitu gabeko egitura mota horien beste adibide bat. Kasu horretan lurrak lau gurpiletako uztai bakoitzean egiten dituen indarrak definitu nahi dira, auto hori gainalde horizontal batean geldirik dagoenean. Indar horiek normalak baldin badira lurrari buruz, lau kopuru eskalar ezezagun ateratzen dira. Gainerako indar guztien eragina -autoaren pisua eta autoaren barruan dihoazenena- normala da lurrari buruz. Beraz, orekaren baldintzak betetzen dituzten hiru ekuazio independente baizik ez daude, bat translaziozko orekarena indar guztien norabide bakarrean, eta bi errotaziozko orekarenak plano horizontal batean elkarzutak diren bi ardatzei buruz. Problema hori ez dago oraingoan ere matematikaren bidez ebatzia. Lau hanketako mahai bat, hanka guztiek zorua ukitzen dutela, autoaren antzeko beste adibide bat da.
Benetako edozein problema fisikok ebazpen bakarra baizik ez duenez, problema hori ebatzi ahal izateko oinarri fisiko bat aurkitu beharra dago indarren arteko erlazio osagarri independenteetan. Kontuan hartuz gero, orain arte egin den bezala, egiturak inoiz ez direla erabat zurrunak izaten, zailtasun hori desagertu egiten da. Izan ere, adibide hauetan aukeratu diren egiturak zertxobait itxuraldatuko dira. Adibidez, automobilaren uztaiak eta lurra itxuraldatu egingo dira, eta eskailera eta pareta ere bai. Elastikotasunaren legeek eta egituraren tasun elastikoek baldintzatzen dute itxuraldatze jakin baten nolakotasuna, eta lau indarrek behar duten erlazio osagarria horien araberakoa da. Beraz, azterketa oso bat egiteko, elastikotasunaren legeak hartu behar dira kontuan, gorputz zurrunen mekanikaz gainera
Gorputz zurrunen oreka egonkorra, ezegonkorra eta orobateko oreka, grabitazio eremu batean
Grabitazio indarra indar kontserbatzailea dela gauza jakina da. Indar kontserbatzaileentzat energia potentzialaren U (x, y, z) funtzio bat defini daiteke non U ondoko aclierazpenen bidez egongo den F indarrarekin lotua
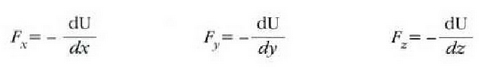
dU/dx zero den puntuetan, indar kontserbatzaile horren eraginpeko zatikia translazio orekan egongo da
x aldagaiaren norabidean, izan ere 0 izango baita  .
Era berean, dU/dy edo dUldz zero direnean, zatiki bat translazio orekan egongo da y eta z aldagaiei buruz,
hurrenez hurren. U funtzioaren deribatua puntu batean zero izango da U balioa puntu horretan muturreko balioa denean
(gorena edo behereena), edo U konstante denean koordenatu aldakorrari buruz.
.
Era berean, dU/dy edo dUldz zero direnean, zatiki bat translazio orekan egongo da y eta z aldagaiei buruz,
hurrenez hurren. U funtzioaren deribatua puntu batean zero izango da U balioa puntu horretan muturreko balioa denean
(gorena edo behereena), edo U konstante denean koordenatu aldakorrari buruz.
U gutxieneko balioan denean, zatikia oreka egonkorrean egongo da; kokagune horretan gertatzen den edozein aldaketak indar lehengoratzaile bat sorraraziko du, zatikia berriro oreka egoerara itzultzeko joera izango duena. Beste era batera esanda, oreka egonkorrean dagoen gorputz baten kokagunea aldatzeko kanpoko eragile bat behar da; gorputzak mugitzean egindako lana indar kontserbatzaileak ematen dio barnetik, eta energia potentziala murrizten da horren ondorioz.
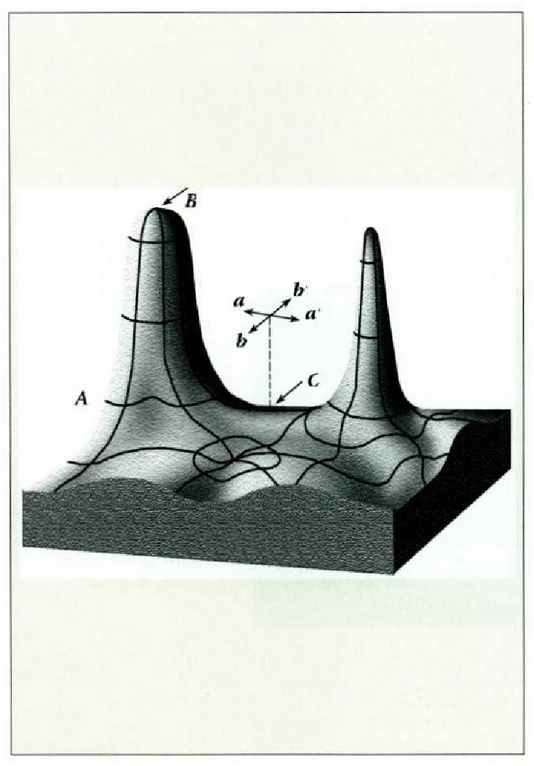
14.8: Grabitazio potentzialeko gainaldea, gainalde errealtzat bar daitekeena. A, B edo C puntuetan jarritako zatiki bat orekan dago; puntu horien plano ukitzailea horizontala da. Puntu horietan zatikia orekan dagoela esaten da. Baldin eta A puntuan zatikia apur bat mugitzen bada, berriro A puntura itzultzeko joera du. A oreka egonkorreko puntu bat da beraz. Baldin eta B puntuan zatiki bat apur bat mugitzen bada, gehiago urrunduko da jatorrizko kokagunetik. Horrenbestez, B puntua oreka ezegonkorreko puntu bat da. Azkenik, C puntuko zatikia apur bat mugitzen bada aa' norabidean, berriro C puntura itzultzeko joera izango du, baina bb' norabidean mugituz gero, mugimendua areagotuko da. C puntuari mendi arroilako puntu esaten zaio, arroilaren itxura duelako. Irudian ez da adierazi zatiki batek edozein gainalde lau horizontalean izango lukeen orobateko orekari dagokion kokagunea.
U konstante denean, zatikia orobateko orekan egongo da. Kasu honetan, zatikia apur bat mugi daiteke inolako aldarapen indarrik eta lehengoratze indarrik jasan gabe.
Zatiki bat koordenatu bati buruz orekan egon daiteke nahiz eta beste koordenatu bati buruz ez egon orekan; hori gertatzen zaio, adibidez, mendi arroila batean dagoen zatiki bati.
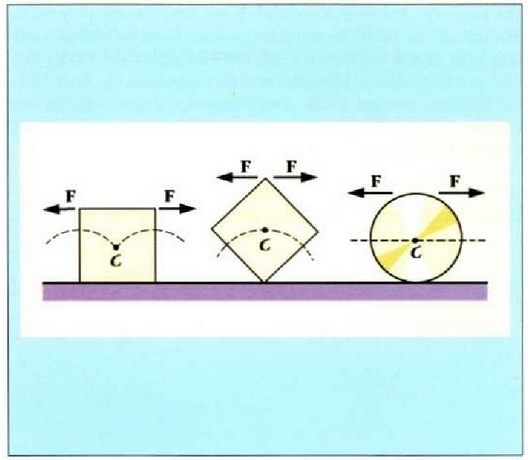
19.9: Kontuan hartzeko moduko gorputz baten oreka. (a) Kubo bat bere aldeetako baten gainean etzana, oreka egonkorrean dago, bere Cgrabitate zentroa igo egiten baita kuboari F indar batek eragiten badio. (b) Kubo bat bere erpin baten gainean dago, oreka ezegonkorrean, C zentroa jaitsi egiten baita F indar batek kuboa apur bat okertzen badu. (e) Esfera edo zilindro bat orobateko egoeran dago, C ez baita ez igotzen eta ez jaisten F indarra aplikatzen zaionean.
Orain arte azaldu dena zatikiei dagokie, hau da, translazio mugimenduari aplika dakioke. Eman dezagun gorputz zurrun bat hartzen dela. Kasu horretan errotazio oreka eta translazio oreka, biak, hartu behar dira kontuan. Baina grabitazio eremu bateko gorputz zurrunen problema askoz ere soilagoa da, izan ere, gorputz zurrun baten zatikiei eragiten dieten grabitazio indar guztiak puntu bati eragiten dioten indar gisa har daitezke, translazio zein errotazio mugimenduei dagokienerako. Orekari dagokionean, gorputz zurrun osoaren ordez grabitate zentroan gorputz haren masaren masa baliokiclea duen zatiki bat har daiteke
Aclibidez, eman dezagun kubo bat dagoela bere aldeetako bat mahai horizontal batean etzana duena. Grabitate zentroa kuboaren zeharretarako epaiaren erdian irudikatu da 14-9 a irudian. Kuboari indar bat aplikatuko zaio, erpin batean zehar ardatz baten inguruan birarazteko, irristatu gabe. Grabitate zentroa goratu egiten da eta kuboaren gainean indarra egiten da, eta horren ondorioz energia potentziala igotzen da. Indarrik egiten ez bazaio, kuboa jatorrizko egoerara itzuliko da berriro, eta bere energia potentzial igoa energia zinetiko bihurtuko cla erortzean. Beraz, jatorrizko egoera oreka egonkorreko egoera zen. Grabitate zentroan ezarritako masa baliokideko zatiki baten kasuan, grabitate zentroak mugimencluan zehar egiten duen ibilbidearen lerro etenaren bidez adierazi da prozesu hori. Zatikiak gutxieneko energia potentziala du oreka egonkorreko egoeran. Horrenbestez, esan daiteke, gorputz zurruna oreka egonkorrean egongo dela baldin eta indar bat aplikatzen zaionean gorputzaren grabitate zentroa goratzen badu baina ezinezkoa bazaio grabitate zentro hori beheratzea
Baldin eta kuboa erpin baten gainean orekan gelditu arte biratzen bada (14-9 b irudia), orduan berriro orekan dago kuboa, baina oreka ezegonkorrean. Izan ere, indar horizontalik txikiena aplikatzen zaiola ere, kuboa erori egingo da eta bere energia potentziala jaitsi egingo da. Grabitate zentroan jarritako masa baliokideko zatikiak lerro etenak adierazten duen ibilbidea egiten du. Oreka ezegonkorrean zatikiak gehienezko energia potentziala du. Esan daiteke, gorputz zurruna oreka ezegonkorrean dagoela baldin eta edozein indar horizontal aplikatzen zaiolarik gorputzaren grabitate zentroak behera egiten badu.
Gorputz zurrun baten orobateko orekaren azalpena emateko mahai horizontal baten gainean jarritako esfera bat hartuko da adibide gisa (14-9 c irudia). Esfera horri edozein indar horizontalek eragiten diola ere, gorputzaren grabitate zentroa ez da ez igoko eta ez jaitsiko, lerro horizontalean zehar mugituko da, besterik gabe. Esferaren energia potentziala konstantea izango da mugimendu guzian zehar, eta grabitate zentroan jarritako masa baliokideko zatikiaren grabitate zentroa ere bai. Sistema ez da mugituko eragin zaion indarra desagertu ondoren. Gorputz zurrun bat, beraz, orobateko orekan dago baldin eta indar horizontal bat aplikatzen zaiolarik bere grabitate zentroa ez bada ez igotzen eta ez jaisten.
9. Hidrostatika
Hidrostatikaren oinarrizko ekuazioa
Isurkari guztiak pisudunak dira, eta horregatik, ontzi batean dauden isurkarietan, goialdeko geruzek behealdekoak zapaltzen dituzte, eta pisuaren ondoriozko presio bat sortzen da horrela. Horrenbestez, isurkariaren puntu jakin batean nolako presioa dagoen, puntu horren gainean dagoen isurkari zutabearen garaierak esango du.
Isurkari batean, isurkari horren gainalde asketik h garaierako distantzian dagoen edozein puntu harturik, ondoko ekuazioaren bidez adieraz daiteke puntu horren gainean dagoen S oinarriko isurkari zutabe zilindrikoak eragiten duen pisuraren indarra:

non zutabearen bolumena V baita eta isurkariaren dentsitatea p. Beraz, pisuak eragiten duen presioari adierazpen hau dagokio:
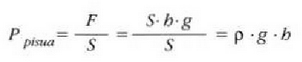

Baldin eta gainalde askeari kanpoko beste presio batek,
 ,
eragingo balio -adibidez eguratsaren presioak eragingo balio-,
orduan h garaierakop presio osoa honela kalkulatuko litzateke:
,
eragingo balio -adibidez eguratsaren presioak eragingo balio-,
orduan h garaierakop presio osoa honela kalkulatuko litzateke:

Ekuazio hori orokortu egin daiteke isurkari batean garaiera desberdinean kokaturiko bi puntu edozeinen arteko Dr presio diferentzia kalkulatu nahi den kasuetan, eta adierazpen hau geratzen da horrela eginez gero:
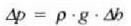
hau da,

Ekuazio horri hidrostatikaren oinarrizko ekuazioa esaten zaio.
Ekuazio horrek adierazten du isurkari jakin batean, kanpoko presioa konstante denean, garaieraren mende soilik dagoela isurkariak jasaten duen barneko presioa. Horrenbestez, maila berean dauden isurkariaren puntu guztiek presio bera jasaten dute. Horrek esan nahi du, ez ontziak eta ez ontzi barnean dagoen isurkari kopuruak ez duela zerikusirik hondoak jasaten duen presioarekin, isurkariaren garaierak bakarrik duela eragina horretan. Paradoxa hidrostatiko esaten zaio adierazpen horri, eta oinarrizko ekuazioaren ondorio gisa hartzen da.

Pascalen printzipioa eta printzipio horren aplikazioak
Ontzi batean dagoen isurkari baten puntu jakin bati aplikaturiko presioa isurkariaren puntu guztietara hedatzen da puntu jakin horretan duen balio berarekin.

Enunziatu horri Pascalen printzipioa deritzo, Blas Pascal frantses fisikari eta matematikariak (1623-1662) egindako ikerketa eta saiakeretan oinarritua baita.
Pascalen printzipioa hidrostatikaren oinarrizko ekuazioaren eta isurkarien
konprimaezintasunaren ondorio gisa interpreta daiteke. Era horretako jariakarietan
dentsitatea konstantea da, eta hortaz, 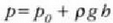 ekuazioaren arabera, gainalde askean presioa igotzen bada, adibidez,
hondoko presioak ere maila berean egingo du gora, p g h ez baita aldatzen h aldatzen ez delarik.
ekuazioaren arabera, gainalde askean presioa igotzen bada, adibidez,
hondoko presioak ere maila berean egingo du gora, p g h ez baita aldatzen h aldatzen ez delarik.
Pascalen printzipioaren aplikazio nagusia prentsa hidraulikoa da, eta aplikazio
nagusia izateaz gainera printzipio horren esanahia argitzeko tresna baliagarria ere bada.
Prentsa hidraulikoaren osagai nagusiak epai desberdineko bi zilindro dira, elkar komunikatuak
eta isurkariz -urez edo olioz, adibidez- beteak. Zilindro horietako bakoitzari epai desberdineko
bi enbolo lotzen zaizkio, isurkaria ukitzen daudela biak.
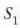 epai txikiena dagokion enboloari
epai txikiena dagokion enboloari
 indarrak eragiten dionean,
enbolo horrek ukitzen duen isurkariari eragiten zaion
indarrak eragiten dionean,
enbolo horrek ukitzen duen isurkariari eragiten zaion
 presioa isurkari guztira
hedatzen da bat-batean eta balio berarekin; beraz, isurkariak
presioa isurkari guztira
hedatzen da bat-batean eta balio berarekin; beraz, isurkariak
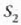 epai txikiena dagokion enboloari
egiten dion
epai txikiena dagokion enboloari
egiten dion  presioaren berdina izango da, hau da:
presioaren berdina izango da, hau da:

hortaz:
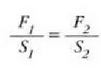
eta:
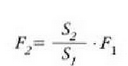
Baldin eta  epaia
epaia  epaiaren hogei
halako bada, enbolo txikiari aplikaturiko
epaiaren hogei
halako bada, enbolo txikiari aplikaturiko  indarra hogei aldiz handiagoa izango da enbolo handian.
indarra hogei aldiz handiagoa izango da enbolo handian.
Prentsa hidraulikoa Arkimederen palankaren antzeko tresna da; indarren intentsitatea anplifikatzeko aukera ematen du eta igogailuen, prentsen, balazten eta industriako tresnetan erabiltzen diren beste hainbat dispositiboren oinarria da.
Elkar komunikaturiko hodienprintzipioa
Elkarrekin komunikaturiko bi ontzi harturik, ontzi horietako batean isurkari bat botatzean isurkaria bi ontzietara zabaltzen da, halako eran non edozein delarik ere ontzien edukiera, isurkariak maila bera baitu bi ontzietan. Hori da, hain zuzen ere, elkarrekin komunikaturiko hodien printzipioa, hidrostatikaren oinarrizko ekuazioaren ondorio.
A eta B maila bereko bi punturen presio hidrostatikoak berdinak dira, hau da:

beraz, baldin eta 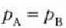 betetzen bada, bataren eta bestearen gainaldeen
betetzen bada, bataren eta bestearen gainaldeen
 eta
eta
 garaierek berdinak izan
behar dute nahitaez, hots,
garaierek berdinak izan
behar dute nahitaez, hots, 
Dentsitate desberdineko bi isurkari nahaskaitz erabiliz gero, isurkari bakoitzaren dentsitatearen
alderantziz propotzionalak izango dira isurkarien garaierak. Horrela, baldin eta
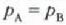 bada, adierazpen hau aterako da:
bada, adierazpen hau aterako da:

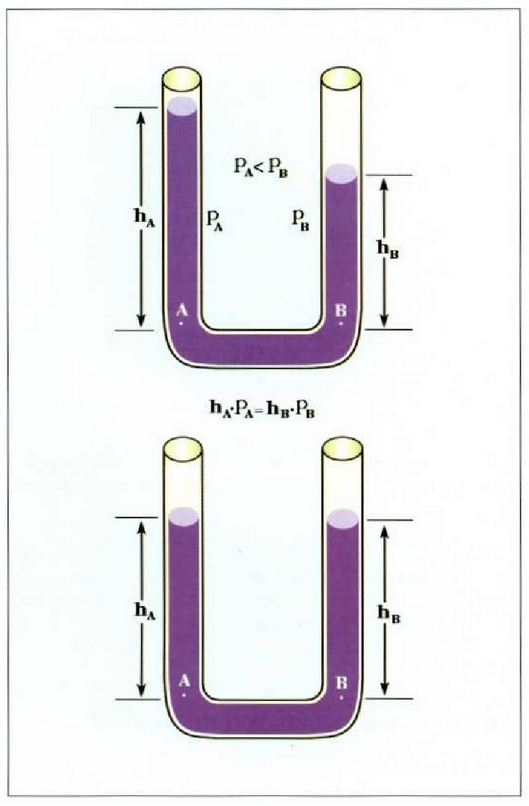
Ekuazio horrekin, garaieren batez bestekotik abiatuta isurkari batek besteari buruz duen dentsitatea esperimentalki kalkula daiteke, eta beraz, nahastu ezin diren isurkarien dentsitateak neurtzeko aukera ematen du, isurkarietako baten dentsitatea ezaguna denean.
Presioa puntu jakin batean
Presioa indarraren eta gainaldearen arteko zatiki gisa definitzen duen adierazpenak gainalde lau bati perpendikularrean eragiten dion indar konstante bati egiten dio erreferentzia. Orekan dauden isurkarietan, presioarekin zerikusia duten indarrak ontziaren gainaldeari buruz zutak dira isurkariaren puntu guztietan; hori delaeta, norabide bereko bi magnitude bektorialen zatidura den magnitude eskalartzat hartzen da presioa; bi magnitude horiek indarra eta gainalde balioa dira, hain zuzen ere. Area izango da bektorearen modulua, eta gainaldearen perpendikularra izango du norabidea.
Indarra konstante ez den kasuetan, hau da oinarri gisa harturiko S gainaldearen
puntu guztietan berdina ez denean, puntu jakin bateko presioa aztertzen da.
Horren definizioa emateko puntua inguratzen duen elementu bat hartzen da,
 gainaldea duena;
elementu horren hedadura asko murriztuz gero, hari eragiten dion
gainaldea duena;
elementu horren hedadura asko murriztuz gero, hari eragiten dion
 indarra konstantea
dela esan daiteke. Kasu horretan, emandako puntuaren gaineko presioari adierazpen matematiko hau dagokio:
indarra konstantea
dela esan daiteke. Kasu horretan, emandako puntuaren gaineko presioari adierazpen matematiko hau dagokio:

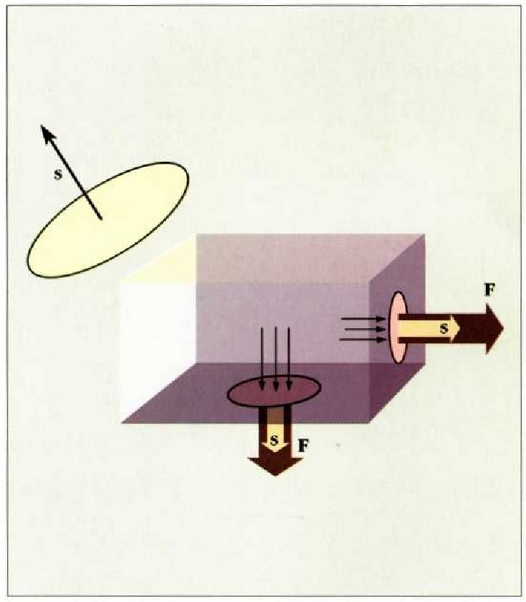
Adierazpen hori -F indarraren deribatua S gainaldeari buruz- da puntu jakin bateko presioaren balioa ematen duena, eta kokagunearen arabera indarra nola aldatzen den adierazten duen ekuazio matematikoaren bidez kalkula daiteke
Baldin eta indarra aldakorra bada eta F bada S gainaldeari eragiten dioten indar guztien ondoriozko indarra, orduan

formulak definituko du batez besteko presioa
Hidrostatikaren oinarrizko ekuazioaren aplikazioa
Urpekari bat 1000 m murgiltzen da uretan. Zehaztu urpekariak jasan behar duen presioa,
eta kalkulatu presio hori zenbat aldiz handiagoa den kanpoan jasaten duenarekin alderatuta,
jakinik itsasoko uraren dentsitatea 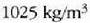 dela.
dela.
Hidrostatikaren oinarrizko ekuazioaren arabera:

Eta kontuan harturik kanpoko p o presioa atmosfera batekoa dela (1 atm =
 ),
datu hauek aurreko ekuazioan ordekatzean adierazpen hau ateratzen da:
),
datu hauek aurreko ekuazioan ordekatzean adierazpen hau ateratzen da:

Kanpoko 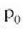 presioa p presioa baino zenbat aldiz handiagoa den jakiteko bien arteko zatidura egin behar da:
presioa p presioa baino zenbat aldiz handiagoa den jakiteko bien arteko zatidura egin behar da:
 aldiz
aldiz